The actual values of  and
and 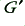 depend both upon the materials chosen for the cables, and the sizes and shapes of the conductors. In general, larger cables tend to have a greater cross section of metal, and a wider dielectric gap, and hence can have lower loss, but this rule can easily be broken if one cable is manufactured with more care than another. The most common metal for cables tends to be copper, but aluminium and steel are also used quite often. Although aluminium and steel have a lower conductivity than copper they are cheaper, aluminium is lighter, and may resist tarnishing (‘rusting’) better. Silver, graphite (carbon), and even gold are used in special cases. Typical values for the resistivity of some of these materials are shown below.
depend both upon the materials chosen for the cables, and the sizes and shapes of the conductors. In general, larger cables tend to have a greater cross section of metal, and a wider dielectric gap, and hence can have lower loss, but this rule can easily be broken if one cable is manufactured with more care than another. The most common metal for cables tends to be copper, but aluminium and steel are also used quite often. Although aluminium and steel have a lower conductivity than copper they are cheaper, aluminium is lighter, and may resist tarnishing (‘rusting’) better. Silver, graphite (carbon), and even gold are used in special cases. Typical values for the resistivity of some of these materials are shown below.
|
| Copper
| Aluminium
| Silver
| Graphite
| Gold
|
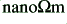
| 16·9
| 26·7
| 16·3
| 13,750·0
| 22·0
|
(In practice, most cable materials are not ‘pure’ and are alloys
with resistivity values which may differ from the above.)
From the table, silver would seem to be the best choice as it has a very low resistivity and hence would be expected to minimise signal losses. Alas silver suffers from two drawbacks. It is very expensive, and tarnishes very easily. Since a surface tarnish nearly always degrades electrical performance this means it should only be used in situations where the surface can be protected from the atmosphere – e.g. by a coating. Copper is much cheaper, and has almost as low a resistivity as silver, hence its popularity, although it, too, will tarnish.
The most commonly used dielectrics are: air (which has the obvious advantage of being free!), polyethylene, ptfe, and pvc. Their main properties are summarised in the table below. Note that is customary to specify the a.c. losses of a dielectric in terms of a value which is called the Loss Tangent ( 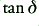 ) or Power Factor (
) or Power Factor (  ). This is a dimensionless number based upon the ratio of the real and imaginary parts of the material’s dielectric constant.
). This is a dimensionless number based upon the ratio of the real and imaginary parts of the material’s dielectric constant.
|
| Dry Air
| Polyethylene
| PTFE
| PVC
|

| 1·0006
| 2·2
| 2·1
| 3·2
|
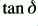
| low
| 0·0002
| 0.0002
| 0.001
|
 (d.c.) (d.c.)
| high
| 1015
| 1015
| 1015
|
| Breakdown ( MV/m)
| 3
| 47
| 59
| 34
|
(The compositions of all these materials varies from sample
to sample, so the above values should be only taken as typical.)
To take these values into account we can define an effective shunt conductivity per unit length value of
and substitute this as required into the earlier expressions for the cable impedance, velocity, and attenuation coefficient.
Looking back to the table of resistivities the inclusion of graphite seems curious. It has a resistivity about 1000 times greater than the other metals that are often used as conductors, hence seems a rather poor choice. In fact, there is a specific reason why a higher conductivity can sometimes be very useful. This is linked to what is referred to the as the Skin Effect.
The Skin Effect arises when EM waves are incident upon, or are guided by, conducting surfaces. The E-fields set up currents in the surface and hence the field only penetrates for a finite distance. This in turn means that the currents only exist near the surface. In practice, in a ‘thick’ conductor the current level falls exponentially with the depth below the metal surface. The result is that the currents on conductors associated with a guided field only make use of a finite metal thickness. Hence the resistance experienced by the currents (which leads to dissipation losses) is influenced by this thickness as well as the material’s resistivity. The magnitude of the current falls exponentially with a 1/e scale depth given – for good conductors – by the approximate expression
where  is the signal frequency, and
is the signal frequency, and 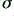 is the conductor’s conductivity. (This expression assumes the conductor is ‘non-magnetic’ – i.e. it has a
is the conductor’s conductivity. (This expression assumes the conductor is ‘non-magnetic’ – i.e. it has a 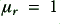 .)
.)
The significant point is that this thickness depends upon the signal frequency as well as the conductivity. The table below gives the skin depth values for copper and graphite at a series of frequencies.
|
| 100Hz
| 10kHz
| 1MHz
| 100MHz
| 10GHz
|
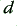 copper copper
| 6·5 mm
| 0.65 mm
| 65 microns
| 6·5 microns
| 0·65 microns
|
 graphite graphite
| 185 mm
| 18·5 mm
| 1·85 mm
| 0·185 mm
| 18·5 microns
|
In general, the wires in many cables tend to have thicknesses or diameters of the the order of 0·1mm to 1mm. Hence when made of copper, we find that the full bulk of the material is only used to support signal conduction for frequencies up to around 100 kHz. At higher frequencies, the cross-sectional area of the material where conduction occurs tends to fall with increasing frequency. The result is that the dissipation resistance per length, 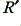 , tends to rise with frequency. This frequency dependence affects both the signal velocity – causing dispersion distortions – and preferentially attenuates high frequencies – causing a change of the amplitude spectrum. Hence it is to be avoided when possible. There are two main ways to avoid these problems.
, tends to rise with frequency. This frequency dependence affects both the signal velocity – causing dispersion distortions – and preferentially attenuates high frequencies – causing a change of the amplitude spectrum. Hence it is to be avoided when possible. There are two main ways to avoid these problems.
The first is to use a material of higher resistivity, such as graphite. This means that a conductor of the same size as before will tend to keep a fairly uniform 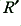 value to a frequency around 1000 × higher than when using copper. The drawback being that the losses will be higher (but more uniform) at lower frequencies. The second method (which is sometimes combined with a change in material) is to use many fine, individually insulated wires in a ‘woven’ arrangement. This means that each individual wire has a small thickness, hence its entire bulk will tend to be used to a higher frequency than for a fatter wire. The snag is that, by having a smaller cross-section, it may have a high resistance. However, by using many such wires all used ‘in parallel’ we can reduce the overall resistance to a low level. For this kind of reason, many co-axial cables use ‘braided’ or woven meshes of many thin wires. Similarly, wound components and wires employed for ‘rf’ purposes sometimes use a woven construction called ‘Litz wire’ after its developer.
value to a frequency around 1000 × higher than when using copper. The drawback being that the losses will be higher (but more uniform) at lower frequencies. The second method (which is sometimes combined with a change in material) is to use many fine, individually insulated wires in a ‘woven’ arrangement. This means that each individual wire has a small thickness, hence its entire bulk will tend to be used to a higher frequency than for a fatter wire. The snag is that, by having a smaller cross-section, it may have a high resistance. However, by using many such wires all used ‘in parallel’ we can reduce the overall resistance to a low level. For this kind of reason, many co-axial cables use ‘braided’ or woven meshes of many thin wires. Similarly, wound components and wires employed for ‘rf’ purposes sometimes use a woven construction called ‘Litz wire’ after its developer.
The woven arrangement for coaxial cables also has the effect of making them more flexible. This is convenient when we want to bend them to fit around corners. However it also increases their sensitivity to Microphony. This is an effect where any changes in external force (or atmospheric pressure) applied to the cable tends to alter its outer diameter, or shape. This will change its capacitance per length. Now the cable’s conductors must be charged when there is a potential difference between them. Altering the capacitance can’t immediately create or destroy charges, so the potential difference changes. The result is that the voltage between the inner and outer conductor changes in response to pressure.
In some cases a coaxial cable may be deliberately given a large steady charge, and then the voltage between its inner and outer conductors measured. The result is a linear ‘capacitor microphone’ which can be used to detect soundwaves, bending of the wire, or even footfalls, anywhere along the cable. A particular use is in the security industry where such a system can be used as an intruder detector in any location where the wires are laid. In other situations this microphonic behaviour is a potential problem. For example, it would be undesirable in cables used as part of a home hi-fi as it would mean that delayed sound signals might be picked up radiating from loudspeakers when music is being played at high level. This could then be re-amplified and appear as a form of ‘echo’ or acoustical feedback, altering the total sound pattern being produced.