As with music, the detailed designs of loudspeakers and their crossover units vary a great deal from one example to another. This means we have to choose an example, and bear in mind that it may not represent every case. For the sake of example here I have chosen to assume that the crossover is of a simple second-order form, with a relatively low cross-over frequency in order to maximise the amount of power that may end up being sent to the tweeter – irrespective of whether it may come from clipping or compression effects.
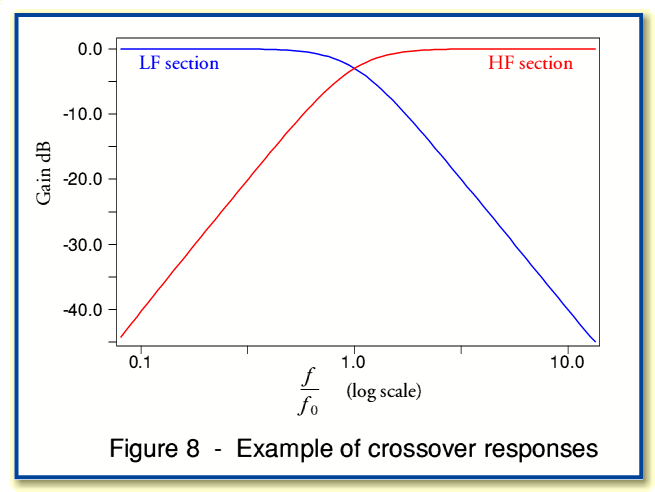
To see why the details of the cross-over arrangement may matter we can start by considering the frequency response graphs illustrated in figure 8. The represent a simple second order pair of high-pass and low-pass filters, designed to share the total input power between the two speaker units. The red line indicates the response of the filtering this produces between the speaker input and the tweeter, the blue line shows the response of the filtering between the input and the woofer.
The horizontal scale is logarithmic, and shows the signal frequency relative to the nominal cross-over dividing frequency value,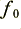 
. A simple view would be to assume that any signal power at frequencies above 
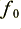would be directed to the tweeter, and any signal power below 
would be directed to the woofer. However the actual cross-over does not perfectly divide the power in this way. At frequencies which are near to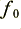 
the power is divided, with some going to the ‘wrong’ unit.
The precise details will vary a great deal with the choice of cross-over behaviour. However in the case used here as an example we can draw up the following table of example values for the power division at a few example frequencies.
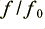
| 1·0
| 0·8
| 0·6
| 0·4
| 0·2
|
| HF section gain (dB)
| –3·0
| –5·4
| –9·4
| –16
| –28
|
| Power for 100 Watts in
| 50
| 28
| 11.5
| 2·5
| 0·15
|
The key point can be seen by considering the lowest row of the above table. This indicates how much power would nominally be directed towards the tweeter when the input is a 100 Watt sinusoid of the relevant frequency. We can see that once the frequency is around a half of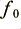 
or more then over 10 Watts of this might be directed to the tweeter – even though the crossover is seeking to divert these signal components to the LF unit. As a result it may be that we should bear in mind the possibility that such ‘leaked’ LF power may play some role in any tweeter damage that occurs when high power levels are used.
For example, in a situation where the LF signal power levels are, say, ten times greater than the HF power levels, then we might sometimes find that the power delivered to the tweeter as a result of unintended LF leakage was comparable with the intended HF power level. Thus – in principle at least – we might need to take this into account when considering the total power presented to the tweeter. It may therefore not be sufficient just to consider only the power above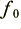 
when assessing the possibility of tweeter damage. Whether this factor is significant will depend upon the details of the actual cross-over, the speaker units, and the music being played. Hence it is hard to say how often (if ever) it contributes to any damage.
At this point it is also worth bearing in mind that tweeter damage may not occur purely due to the tweeter becoming overheated. This may weaken the tweeter and make it more susceptible to damage for some other reason. Two possibilities are:
- Excessive displacement.
- Excessive accellerational forces.
In normal use, the vibration of the tweeter will require significant accelerations and forces. It may be that the peak levels which a unit can endure fall as the unit is heated, and this may mean the unit is damaged by brief peaks in the signal which would not cause a problem if the unit was at room temperature. It might be the case that the peak levels when the signal is clipped are not higher than when it is unclipped, but that the higher mean power means they are more likely to cause damage during sustained clipping.
In normal use, most conventional drive units are operating over most of their frequency range in a “mass limited” manner. This means that the amplitude of the movements which are produced by an input signal of constant size will tend to increase when we reduce the signal frequency. The simplest physical model for this is as follows:
1) We assume that the amplitude of the input signal sets the level of acceleration or force applied to the speaker unit, and that this relationship is nominally independent of frequency. This means that when we change the frequency, keeping the amplitude the same, the acceleration remains the same.
2) Lowering the frequency means that each half-cycle of the oscillation lasts longer. This means the acceleration during each half-cycle lasts longer, but from (1) has the same amplitude profile. Since the velocity attained will depend upon the amount of acceleration, and how long it is applied, this implies the velocity of movement produced will rise in inverse proportion with the frequency. i.e. halving the frequency will double the speaker unit velocity attained.
3) The displacement of the speaker unit will depend upon the velocity reached, and how long this persists during each half-cycle. Hence by the same argument as (2) we could expect the same peak velocity at a lower frequency to produce a larger displacement. As with (2) there is an inverse proportionality.
4) Combining (2) and (3) implies that the speaker displacement will – for a constant amplitude of electrical input – varies as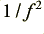 
. i.e. if we halve the frequency, for a given signal size, we can expect the displacement to increase by a factor of 4. If we reduce the frequency by a factor of 10, the displacement could become 100 times larger!
In itself, this could be expected to produce an output sound level that rises as we lower the frequency. However this is counteracted by the cross-sectional size (diameter) of the speaker cone/dome being small compared with the wavelength of the sound which the unit is trying to radiate. This means the efficiency of the unit (in terms of the amount of sound power radiated for a given speaker displacement or movement) tends to rise with frequency. In practice, a speaker designer will engineer these two effects and seek to cancel one against the other in order to produce a more uniform output sensitivity.
The result is that a mass-controlled speaker unit produces smaller displacements at higher frequencies, but the improved efficiency means we get an output that remains in proportion with the electrical driving signal over a reasonably wide frequency range. However this may mean that low frequency signals may produce very large speaker displacements even when the resulting sound output level from the unit is low.
At some low frequency value the unit will cease being mass controlled, and the size of any displacements will then become limited by the forces exerted by the suspension (or air behind the unit). However the result of the overall design may be that unintended LF may produce large movements. Here we are assuming a second-order crossover network. This means that, at low frequencies, the HF section tends to reduce the amplitude of the electrical signal seen by the tweeter by a factor of 4 each time we halve the signal frequency.
If we now combine this with the above argument we arrive at a conclusion that is perhaps surprising. For an input electronic signal that contains similar amplitudes at LF and HF we may find that – when using a second order cross-over and a mass controlled tweeter – the tweeter may undergo displacements from the LF which are similar in size to those produced by the HF. The resulting output LF power will be small because the tweeter will be a very inefficient radiator under these conditions. However any large displacements due to LF leakage may then be a factor in mechanically stressing the speaker unit.
As with the accellerational forces, when a unit is heated it may become more sensitive to damage by such a mechanism. Hence ‘leaked’ LF might both contribute to heating the unit, and play a role in mechanical damage. Whether this is a factor will depend upon the details of the speaker design. For example, if the speaker system uses a higher-order crossover, then the signal level presented to the tweeter may be much lower than would be the case for a second order crossover, and hence LF produced displacements may become small enough to become irrelevant.
For the sake of the following examples, the loudspeaker system is assumed to employ a simple second-order crossover system with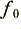 
chosen to be 1·8 kHz. Higher crossover frequency values are common, and would tend to reduce most of the effects being discussed here. Hence a reasonable, but low, value has been chosen to try and make any effects as clear as possible. The results obtained will, however, depend upon this and the choice of music. As a consequence it is always open to question how ‘typical’ the results we obtained may be. The following results should therefore be regarded as interesting, but not necessarily conclusive.
