A quite different explanation of how tweeter might be damaged has been suggested. This does not explicitly rely upon clipping, but seeks to explain the problem by attempting to use a more realistic model of musical waveforms.
Musical waveforms are often quite complex, and may simultaneously contain both LF and HF components, or may alternate between sections dominated by LF or by HF. Statistically, the mean power levels at frequencies in the few hundred Hz range tend to be greater than at higher frequencies provided we take a long-term average – although transient musical events may briefly produce quite high HF power levels. Initially, let us concentrate on waveforms where HF and LF are simultaneously present. Later on we can return to what may happen when they occur separately.
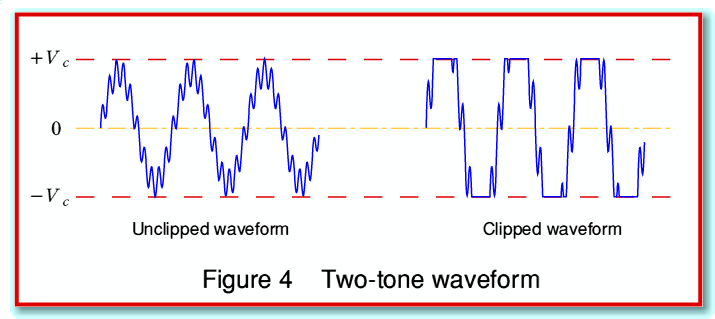
On the above basis a slightly more ‘realistic’ model of an example waveform would be one that simultaneously contained two frequencies - a LF component and an HF component - with the LF component having an amplitude that was noticeably greater than that of the HF component. A wave like this is illustrated in figure 4.
On the left of figure 4 the new waveform is shown at the size which just fails to be clipped. On the right, the intended size of the waveform has been increased to the point where some clipping is evident.
Simply speaking, the alternative argument goes as follows:
Since the LF component of the waveform is relatively large, it is clipped quite noticeably during each half-cycle as it tries to reach its peak positive and negative values. The HF component, being smaller, tends to appear unclipped during large sections of the waveform. Since both components have been amplified, we might then expect the actual resulting increase in the HF level to be more than that for the LF. In one article available on the web that puts forward this argument, this process is described as a form of “compression”. The implication is that the rise in HF level is less affected by the clipping than the rise in LF level. The assumed result is that the spectrum is “compressed” and the difference in HF/LF power levels will reduce when the musical waveform is being clipped.
On the basis of the above, the alternative proposal would be that it is the HF energy in the original musical signal that can produce tweeter damage as the clipping of the LF section of the waveform (it is implied) leaves the HF relatively unaffected. Hence when we turn up the signal level we find that the HF in the musical signal becomes powerful enough to do damage, despite the LF power level being limited by clipping. This result is essentially the same as if we had a much more powerful amplifier that did not clip. We could then wind up the gain and produce an output musical waveform which was unclipped, but which contained too much HF power for the tweeter to endure.
As with the traditional (creation of harmonics) explanation, this argument seems perfectly plausible in general terms, and seems also to be based upon a waveform that is seems more realistic than a single sinewave. However we still need to ask if the actual behaviour is as claimed, and if it is representative of real music, etc.
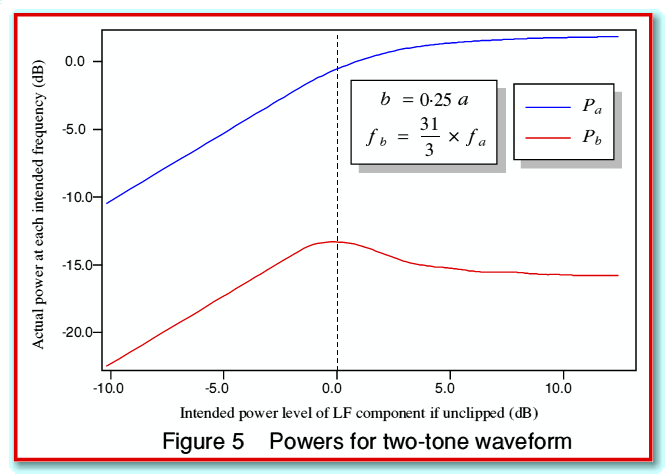
To test the actual behaviour we can consider a specific example. For analysis purposes I settled upon a composite waveform where I could choose the relative amplitudes and frequencies of the two components and then experiment with altering the size of the result and how much it would drive into clipping. A typical result is illustrated in figure 5.
Here the test waveform nominally consists of two sinusoids where the HF component,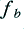 
, has a frequency of 
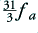, where 
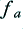is the frequency of the LF component. The amplitude of the HF component 
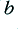, is chosen to be 
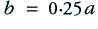, where 
is the amplitude of the LF component. i.e. The HF is around 12dB below the LF when the signal is unclipped, and the HF frequency is just over ten times the LF value. Various other sets of values were tried, and seemed to give results broadly similar to those shown in figure 5.
As with earlier graphs the power levels are in dB referenced to the power level of a single sinewave that would just reach clipping. (e.g. for an amplifier rated at 100 Watts, the 0 dB level represents 100 Watts.) Note that clipping in this case actually begins slightly before we reach the 0 dB level. This is a result of the composite waveform having a different shape to a single sinewave, and the way we have defined the 0 dB level in terms of mean sinewave power. The waveform therefore enters clipping at a lower mean power than 100 Watts.
Well below the 0 dB intended level the plots are exactly what we would expect. The output scales linearly with the gain, with the LF and HF components staying 12 dB apart. The results above clipping are initially more surprising. Here the output LF component level continues to rise, approaching a limit, as we turn up the intended level. However the output HF level falls! Hence for the assumed waveform, this implies that the effect claimed above does not seem to occur. The HF level does not continue to rise once we enter clipping. Instead it falls slightly. The result is to actually reduce the HF level compared with what we would obtain if the signal were only just at the clipping point.
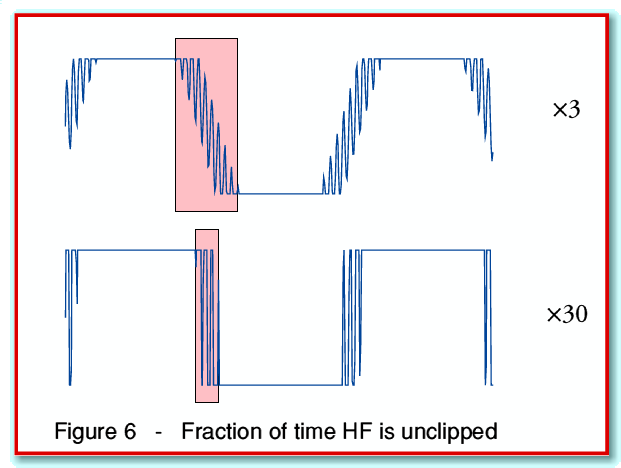
To understand why this is happening we can look again at the effects of clipping such a waveform. In this case we can use figure 6, which compares mild clipping with more severe clipping.
Here a coloured box is used to highlight the period of time during a cycle of the LF component during which the HF is visible. The (relatively!) mild clipping is for a signal whose peak level is three times above the maximum level that would escape clipping. The more severe clipping is times thirty. It can be seen that as the severity of the clipping rises the HF appears for a shorter fraction of the time. This behaviour is analogous to the capture effect familiar to those who work with FM demodulators.
The general result is that although increasing the size of the signal tends to boost the amplitude of the HF when it is visible, it also reduces the fraction of the time when the HF appears at the clipped output. When we consider the mean power over a period of many cycles the result is that the mean HF power does not rise as we wind up the level we are trying to produce.
The above implies that the argument that tweeter damage may be due to the musical HF components survive clipping whilst the HF is limited is of doubtful validity. However, we must bear in mind that the test waveforms used here may still not be a satisfactory model of genuine music. To test this further we require musical examples, but before considering this there is also another factor which may be significant. This is the question of the actual behaviour of the loudspeaker crossover network. We therefore need to take this into account when considering musical examples. Before doing so, however, we should now consider the “compression” proposal in situations where the relative amounts of LF and HF in the waveform may vary with time.
A situation similar to that examined in this section has already been considered at a webpage whose address is http://www.rane.com/note128.html. You may therefore wish to visit this page and read the explanations it presents, and the results obtained there, to compare with what I am discussing here.
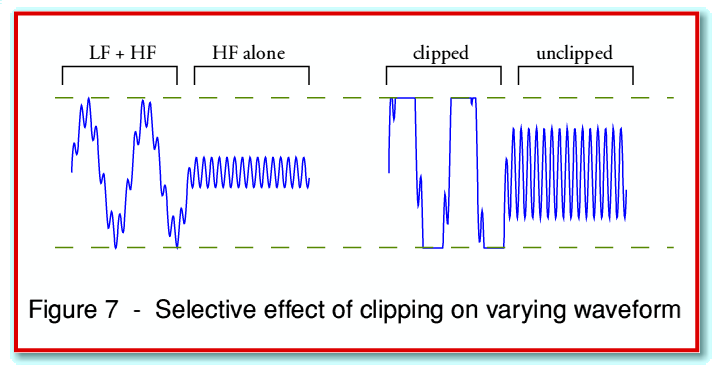
The composite waveform we can use for test purposes now consists of a steady HF component with a burst of LF. Its properties can, therefore, be expected to be midway between the waveform considered above, and a simple single-tone HF. As outlined in the web reference mentioned above, the presence of the HF during the periods when the waveform is not clipped means we may now turn up the desired signal size and obtain an increased level of HF power. This arises from the periods of time when the LF is absent, and hence the enlarged HF is not affected by clipping. This process is illustrated in figure 7.
Provided that the example waveforms used here are representative of real music, and the crossover acts to send all the HF to the tweeter, then the above argument makes it plausible to think that damage may occur due to the “compression” behaviour where large LF bursts are clipped, but separate HF tones are not. It seems doubtful that simultaneous LF and HF would act in the same way due to the behaviour outlined above of the clipped composite waveform. In practice we might expect some mix of behaviours where HF present during periods where the LF+HF were clipped would tend to produce a fall in the mean HF level, but the periods where HF alone were present would tend to produce a rise in the mean HF level. The result would clearly depend upon the details of any actual musical waveform.
The above does not establish that the “compression” is the actual cause of damage in any/most/all cases. Nor does it establish that the commonly assumed mechanism of HF creation via clipping is never or rarely the real cause. From the analysis done earlier it is clear that clipping can generate quite significant levels of HF power. At this point either mechanism seems possible.
In order to help assess the plausibility of each possible mechanism as the cause of damage we need to consider the behaviour of crossover networks and the properties of real music.
