For this section I chose a specific musical example. This was the song “Meet me at the delta” which is a track on a CD made by The Duke Robillard Band and Susann Forrest (“Turn It Around” Rounder NETCD23/CDAM1016). The choice can be considered entirely arbitrary in ‘scientific’ terms as I have no real reason to feel it is more or less ‘typical’ of the music people play than anything else. It is just that I personally find the CD to be quite well played and recorded, so find it enjoyable. I have also used it for some other analysis purposes for much the same reasons.
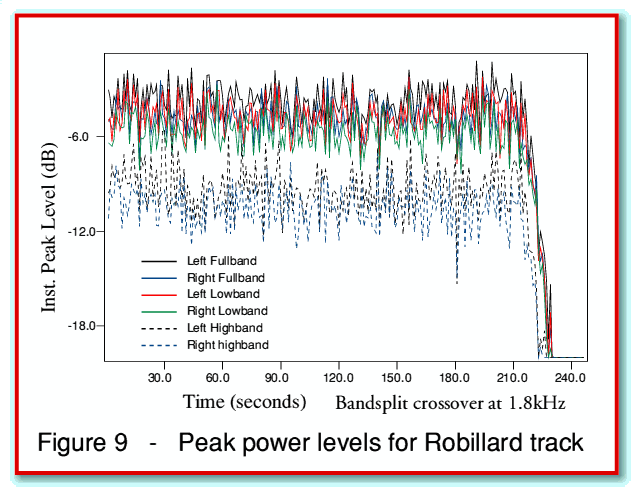
Figure 9 shows six plots, each indicating a nominal peak power level during a series of 1 second intervals. (The levels were obtained by taking the sample level values from the CD and squaring each nominal level to obtain a result proportional to the power at that instant, then normalising the result against the maximum possible sample value squared.) Two lines show the left/right peak power found during each second for the ‘raw’ signal. Two more lines show the left/right peak powers after passing the signal through a numerical filter that simulates a 2nd order low-pass, and the final two after the complementary filter for a 2nd order high-pass. Note that in general in the following analysis I will concentrate upon the mean power (not peak instantaneous) during each time period, and will only show on channel to provide graphic results which are easier to read. I will also limit the analysis to the first half of the track, again for clarity.
Looking at figure 9 we can see that – for this example at least – the peak HF power level directed to the tweeter tends to be around 6dB below the peak LF power level. As a consequence of the comments made earlier about the possibility of “leakage” of LF through the cross-over filter some of this may be unintended LF power reaching the tweeter.
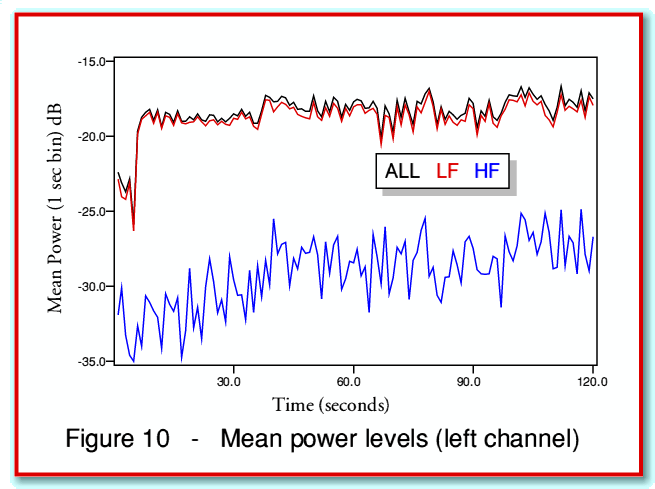
Figure 10 shows similar results, but for the mean power during each one-second period. The results plotted are for the left hand channel only during the first 120 seconds of music. Comparing figure 10 with figure 9 we can note two distinctions between mean and instantaneous peak power plots.
The first difference is that when considering mean levels we find that the HF power is generally around 10 - 12 dB below the LF level, whereas when considering peak levels we find that the HF is more like 6 dB below the LF most of the time. Where we are concerned with damage due to overheating, then it is the medium term mean power levels that may be significant. For that reason we will use mean powers from now on. However it is worth bearing in mind that if damage were to take place for other reasons – e.g. due to excessive accelerational forces, then it is the peak levels that might need to be taken into account.
The second difference to note is that the peak power level of the complete signal during each second tends to be in the -3 dB to -6 dB range, whereas the mean power is more like -18 dB. Figure 10 shows the input power in black, the LF power in red, and the HF power in blue. The 0 dB level here corresponds to the sinewave power that would have the maximum amplitude we can obtain from 16-bit (CD standard) samples. This is distinct from Figure 9 where 0 dB corresponds to the peak power possible for a 16-bit CD sample value. This difference is partly due the different definitions of the 0 dB level in each case, but is mainly due to the shapes (form factor) of the musical waveforms. This mean the peak level can be expected to be somewhat higher than the mean level. It is quite common for musical waveforms to exhibit peak power level around 15 - 20 dB above their short-period mean power levels.
As before we can use the example of an amplifier that would just clip a 100 W mean-power sinewave. We can then assume that the system starts off with a gain chosen so that the maximum levels available from 16-bit CD would just fail to clip the amplifier. Hence the peak and mean power levels for our “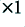
” gain would be as shown in figures 9 and 10. Note that on this basis, the signals of our musical example would peak at around 3dB below the clipping point at this gain.
Figures 9 and 10 then imply that for our initial gain the mean total power will only be a few watts, and the mean HF power will be less than a watt. This is distinct from the peak HF levels which will briefly be tens of watts. Given a tweeter than can handle sustained powers of the order of, say, 5-10 Watts, these unclipped levels are unlikely to lead to any problems.
Figures 9 and 10 are based upon the unclipped signal patterns as read from a CD. We can now simulate clipping and filtering as follows:
- Take the initial signal values and scale them up by a chosen amplitude gain factor.
- Clip the result by limiting any values which exceed the max/min range for 16-bit CD to the maximum/minimum permitted values.
- HF/LF filter the clipped waveform to obtain results for the signals directed to the speaker units.
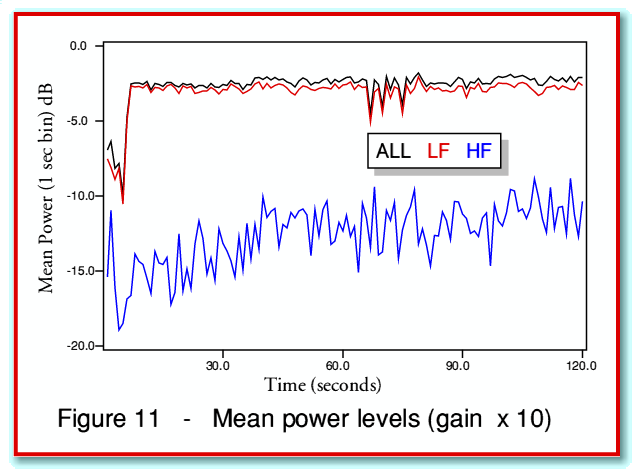
The results of doing this with a gain factor of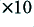 
are illustrated in figure 11. In the absence of any clipping we would expect this simply to raise all the mean power levels by 20 dB. In practice the signals clip for approximately 35% of the period being observed, and this limits the rise in power levels to less than 20 dB. As a result, the mean power levels for the total clipped signal and the LF section rise by around 16 dB, and the HF rises by a similar amount. Simply comparing Figures 10 and 11 by eye it is difficult to see if there has been any overall change in the LF/HF distribution of the mean powers. The only obvious effect is that the powers seem to rise by around 4 dB less than would be the case if no clipping had occurred.
For our 100 Watt amplifier example, figure 11 implies we would have mean HF power levels of around 5 - 10 Watts. Depending upon the loudspeaker design, this might be high enough for sustained use under the conditions assumed to cause damage to the tweeter.
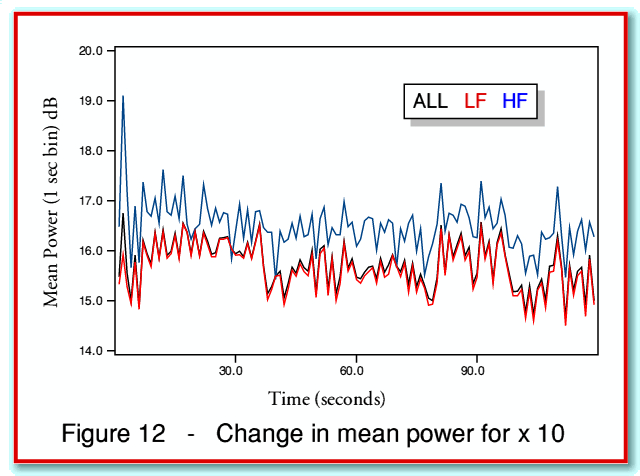
Figure 12 gives a clearer view of the changes in mean power which occur when we increase the gain by a factor of 10 in amplitude terms. Here the plotted lines show the changes in the power levels (i.e. the differences in levels between fig 10 and fig 11). From this set of graphs we can see that a change that would be 20 dB in the absence of clipping turns out to be around 15 - 16 dB for the overall signal and the LF section, but 16 - 17 dB for the HF section. Broadly speaking we can say that clipping has compressed the overall power level by around 4 dB, but the relative amount of HF has risen by perhaps 1 dB. Thus it would seem that the rise in HF level is limited by clipping by almost as much as the LF level.
Indeed, one striking feature of the above is that the change in the relative levels at HF/LF is surprisingly small given that we are clipping around 35% of the time and that the overall compression is more than 3 dB – i.e. the mean power is being held to less than half the value it would have in the absence of clipping. In principle we could expect both harmonic generation due to clipping and any “compression” of alternating LF/HF sections to result in a rise in the relative HF power level. However in this example any such result seems quite modest.
Having obtained the above result it occurred to me that it might be a consequence of choosing a relatively high degree of clipping which may be atypical. Indeed, from figure 9 we can see that the peak HF level is only around -10dB below clipping before we increased the gain. Hence even though the mean HF level was around -30 dB before we increased the gain, it may be that the small change in LF/HF relative levels is due to our seriously clipping the HF as well as the LF in a way that does not occur at lower gains.
To test this hypothesis, I repeated the above modelling for smaller gain factors. However the results simply showed that any difference between the degree of HF and LF compression fell swiftly as the gain was reduced and the waveform spent less time being clipped.
