For our 100 Watt amplifier example, the squarewave approximation implies that when we try to play a sinewave well into clipping the result can be expected to be an output of around 162 Watts at the intended frequency. This is accompanied by approximately 18 Watts at three times the frequency, 6·5 Watts at five times the frequency, 3 Watts at seven times the frequency, and so on with smaller amounts at yet higher frequencies. The result of clipping can therefore be seen to be that a significant amount of power is generated at frequencies higher than intended. The power levels quoted here are all mean (time averaged) levels since our definition of the amplifier as being “100 Watt” is in terms of its unclipped mean sinewave power capability.
The above shows that when we clip a sinewave the mean power at the fundamental frequency will be greater than for the unclipped waveform. Some authors seem not to notice this, and that the squarewave has more power in its fundamental component than is the case for a pure sinewave of the same peak size. This result arises from the factor of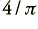 
in the expression for a squarewave’s amplitude. As a result, we must be careful to consider any powers in terms of the mean (time averaged) values, scaled with care against the relevant reference levels.
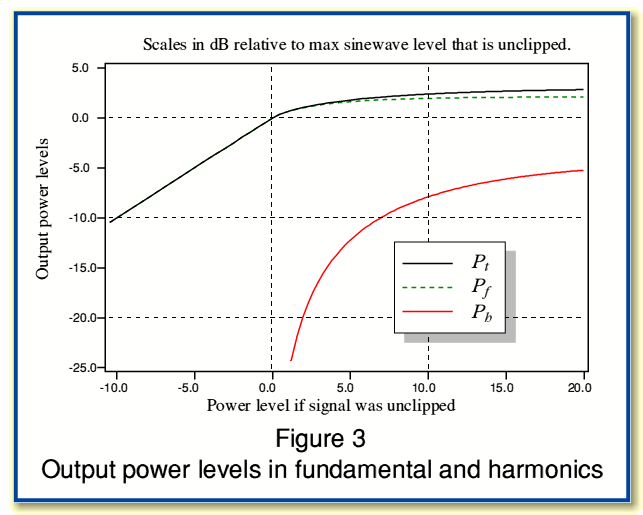
We can get a more general view of how much unintended HF power is created by comparing the total mean power of the clipped waveform with the amount of power present in its fundamental component. This is plotted as a function of the degree of clipping in figure 3.
The scales in figure 3 are in decibels relative to the mean sinewave power that just fails to clip the amplifier. Hence 0 dB on both scales is the clipping point. Below 0 dB the output power scales as we would intend, and no harmonics or distortion are evident. Above 0 dB the output is clipped. The horizontal scale is the power we would obtain for the sinewave if no clipping occurred. The vertical scale shows the actual power output.
The graph in figure 3 shows three curves.
-
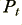represented by a black line. This shows the total output power of the clipped waveform.
-
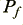represented by a broken green line. This shows the power output at the intended sinewave frequency, 
.
-
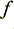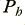represented by a red line. This shows the combined power of any harmonics present at frequencies other than 
.
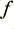For the example of our 100 Watt rated amplifier the 0 dB levels correspond to 100 Watts. The +10 dB point on the horizontal line represents an attempt to obtain an output of 1 kW – i.e. an increase in the intended signal amplitude of around ´ 3·16. In this situation the power in the harmonics will be -7·84 dB referred to 100 Watts – i.e. around 16 Watts. At the + 6 dB clipping point on the horizontal scale we would be attempting to produce an output whose amplitude was around ´ 2 greater than can be produced without clipping and the level of harmonics would be around - 11 dB – i.e. around 8 Watts.
The traditional argument for why the above may lead to tweeter damage can be understood by considering a ‘worst case’ scenario as follows:
Let us assume the desired musical waveform is essentially a loud sustained sinusoid at a frequency of, say, 500 Hz, and that the loudspeaker has a crossover that splits HF from LF at about 1 kHz so that any signal components above 1 kHz are directed to the tweeter. Let us also assume that we are using a 100 Watt amplifier, and the speaker is also rated in musical terms as being “ 100 Watt”, but uses a tweeter than can only endure around 10 Watts for periods longer than a few seconds.
If we now turn up the volume so that the amplifier is clipping the waveform by a factor of around ´ 3 or more, then the harmonic power this creates may be greater than the tweeter can endure for an extended period. Hence the tweeter may then fail as a result of the unintended high levels of HF power which the clipping created.
This argument is plausible if we accept all the assumptions involved. However it is reasonable to question how well they actually describe situations that typically occur. We can, for example, wonder if such levels of clipping would be sustained in any normal domestic musical use without going unnoticed by the listeners and prompting them to turn down the volume due to the high levels of distortion. That said, it is perhaps surprising how easily clipping distortion may be accepted in some cases, although overdriving to the extend of ´ 3 or more does seem excessive for anything except rare/brief occurrences.
We can also question the choice of frequencies in the example above. A typical speaker system may have a crossover that splits HF from LF at a much higher frequency than 1 kHz, and the bulk of the LF signal power with real music may be below 600 Hz. This may mean that a significant fraction of the harmonics generated by clipping will occur at frequencies below the cross-over. Hence the total power they present to the tweeter may be less than assumed above.
More serious doubts may also be presented in two other areas. One is that it is questionable how reliable it is to assume that music is essentially similar to a single, loud, sinewave component. Another question is regarding the actual behaviour of a real crossover arrangement which may not have the idealised behaviour assumed above.
