Many loudspeakers employ two drive units. One is designed to deal with the low frequency (LF) components of the musical signal and tends to be called a “woofer”. The other is physically smaller and is designed to deal with the high frequency (HF) components and tends to be called a “tweeter”. The loudspeaker system also includes a “crossover network” whose task is to direct LF signals to the woofer and HF signals to the tweeter. The details of the crossover, and the precise range of frequencies directed to each unit vary a great deal from one design to another. However in typical cases the dividing line between HF and LF tends to be drawn somewhere between around 1kHz and 5kHz.
Tweeters need to be agile enough to respond swiftly to the high frequency signal patterns. This means they tend to be small and light. As a consequence they also tend to be more flimsy than woofers in terms of their ability to handle high sustained power levels without damage. Thus it is relatively easy to damage some high-performance tweeters by the accidental application of high levels of sustained HF power. Even in loudspeaker systems which are rated for use with 100 Watt amplifiers it is not unusual for the tweeters to only to be able to handle sustained levels of around 10 Watts or less.
Under normal circumstances, most music does not contain high sustained levels of high frequency power. Hence in normal use, all being well, the relative delicacy of the tweeters does not matter. Unfortunately, despite this general observation, sometimes tweeter units do fail. The question is, why?
Clipping
The traditional conventional view is based upon a consequence of a problem called “clipping”. This arises because, for any real device or system, there will be a finite maximum output level which it is able to produce. For an amplifier this typically appears in the form of the amplifier being unable to produce output voltages or currents above given values. The precise values will vary from one amplifier to another, and also to some extent with the conditions of use. However there will always be a limit. Hence if we try to ‘turn up the volume’ too far then we find that the loudest sections of the signal will be clipped.
For the sake of illustration we can consider the situation where we are using audio power amplifiers which can only just provide output voltages up to the level required for a 100 Watt (mean power) sinewave into an 8 Ohm resistive load. (It is common practice to specify the power ability of an amplifier in terms like these. Hence it is convenient to use this approach here.) The mean power of a waveform when presented to a resistive load tends to be proportional to the rms voltage level of the waveform. We can then use the expression
to link the mean power,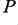 
, with the rms voltage, 
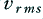, and the load resistance, 
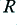. The peak (maximum) voltages required will depend upon the shape of the waveform. For a sinewave, the peak levels (positive and negative) will be such that
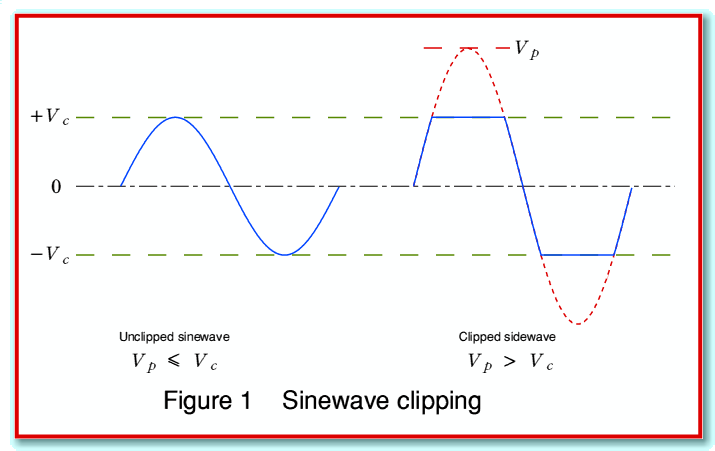
Hence if we use the example of 100 Watts into 8 Ohms we can expect the amplifier to be able to output sinusoidal waveforms with an rms voltage is up to 28·28 Volts, and peak voltages up to ±40 Volts. Any attempts to produce a larger output may fail as illustrated in figure 1.
On the left of figure 1 the amplifier is being asked to output a sinewave whose peak amplitude is just equal to the maximum level,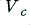 
, which it is able to produce without clipping. On the right we have increased the size of the desired sinewave so that its intended peak size, 
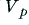, is larger than 
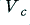. In this example, for the sake illustration, the waveform chosen has 
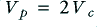. The result is clipped off at the levels 
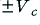to produce flats at the top and bottom of the waveform.
Since the clipped waveform no longer has the shape of a sinusoid it cannot be a pure sinewave at a single frequency. For the symmetric clipping shown, it now has a set of components at the frequencies,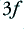 
, 
, 
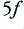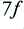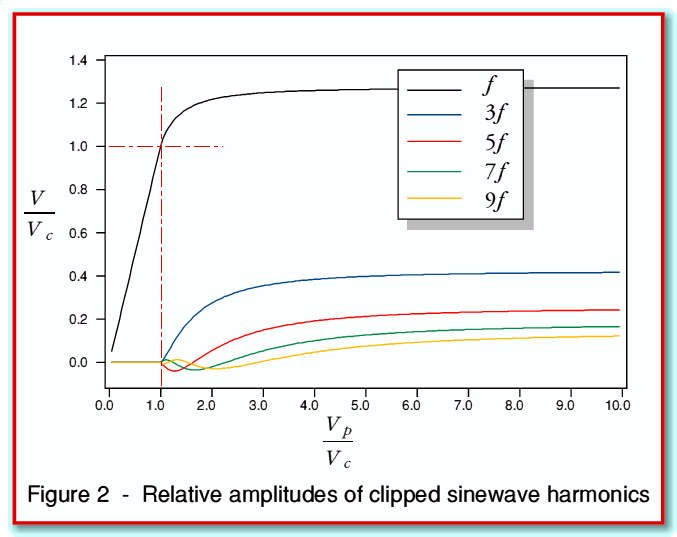
, etc, where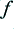 
is the frequency of the sinusoid which the amplifier would produce if the shape were not clipped. Figure 2 shows how the relative amplitudes of these components vary with the degree of clipping. The horizontal axis shows the nominal size of the output sinewave if it were unclipped normalised to the clipping level. The vertical axis shows the sizes of any output components, again normalised to the clipping level.
On both scales, below 1·0 the waveform is unclipped. Hence in this region there are no harmonics, the output waveform is unaffected, and the output level scales up linearly as we would wish. Above 1·0 on the horizontal axis the waveform will be clipped, changing its shape. This tend to limit any increase in the amplitude of the output at the intended frequency (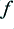
) and to create components at the odd harmonics. The graph just shows the first few harmonics.
As we increase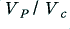 
the resulting waveform approaches the shape of a squarewave. If we consult a suitable book we can find that a squarewave can be written in terms of a series of sinusoidal components of the form
where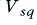 
is the peak level of the squarewave. Once the waveform is large enough for clipping to convert it into a shape indistinguishable from a squarewave we can set 
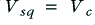and use the above expression to calculate the spectrum of the resulting waveform. We can then draw up a set of amplitudes and powers for the first few components as shown in the table below. Note that in each case the amplitude and mean power are relative to a sinewave of peak size 
.
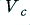| frequency
| 
| 
| 
| 
| 
|
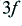
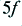
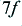
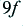
| amplitude
| 1·2732
| 0·4244
| 0·2546
| 0·1818
| 0·1414
|
| power (dB)
| +2·09
| –7·44
| –11·88
| –14·80
| –16·99
|
Looking at figure 2 we can see the levels of the harmonics do approach these values once the value of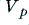 
is a few times greater than 
.
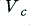Before moving on, it is worth making a few points about the nature of clipping in real amplifiers, with realistic musical waveforms. The first point to note is that with many real amplifiers the values of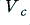 
are not constant, but may vary under load. Thus the clipped top and bottom of the waveform may not be ‘flat’. They may be sloped in some way, or have patterns due to – for example – ripple from the power supply. The second point is that clipping may not be symmetric. The amplifier may be limited to differing extents in the positive and negative directions. The musical waveform itself may be asymmetric, or have an added d.c. offset. Some amplifiers are also powered by a single rail voltage, and hence the symmetry of clipping may alter if sustained. Hence the actual clipping behaviour of a real system may be much more complex than assumed here. Despite these details, the basic behaviour should usually be similar to that described above for most well designed amplifiers. It therefore seems reasonable to use the simple ‘flat top’ clipping model for the analysis in these pages.
