3. Twin Feeder Loudspeaker Connections – an example
These internal values can now be used when we wish to evaluate the effect of a cable upon the transmitted signals. We can treat the connecting cables as a form of transmission line, and modify the inductance and resistance per unit length to take the internal values into account. At audio frequencies the cables are normally many orders of magnitude shorter than the highest signal wavelength so it is reasonable to then use lumped values which just multiply the per-unit-length value by the chosen length. For the sake of example here we will consider loudspeaker cables nominally in the form of ‘twin feeder’. For a given cable length this means we must remember to double the values for internal resistance and inductance as a pair of wires are used.
For illustration we can use a case where we have copper cables (assume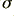 
= 5·8 × 107 mhos/metre) which have wire radii of 2mm with their centers 6·5mm apart. We can also take as an example a twin feeder length of 3 metres. (i.e. 6 metres of wire, in total, in the circuit) and assume a nominal load of 8 Ohms. We can also assume a perfect voltage source and set the source resistance to be 0 Ohms. The cables are assumed to be insulated with a dielectric whose relative permittivity value is 1·5. Most practical dielectrics tend to have a higher value, but the effect is diluted since part of the surrounding E-field is in the air, so this value seems a reasonable one to assume for the purposes of an example.
The results obtainable for this situation are indicated in the following graphs. The dimensions chosen for the wires here are not meant to represent any specific cable, but seem typical for a relatively inexpensive form of wiring.
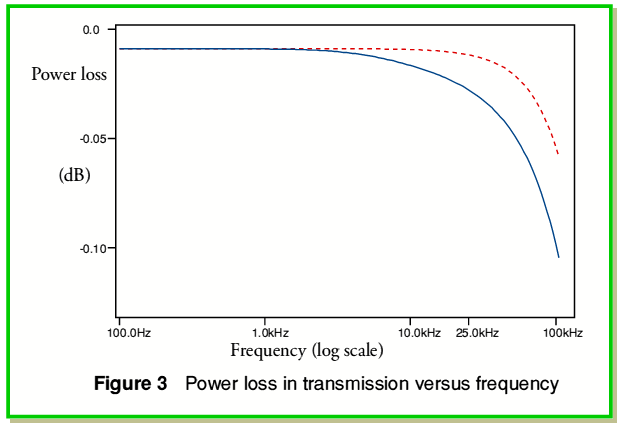
Figure 3 shows the power loss in the cable as a function of frequency. The solid (blue) line shows the loss when the wire’s internal impedance is taken into account. The broken (red) line shows the loss that would occur if we ignored the internal impedance. Hence the difference between the two shows the results in this case of ‘skin effect’. In principle, the broken line shows what we might expect when using wires of ‘Litz’ construction with a fill factor approaching unity. The solid line shows what we might expect from either a solid wire or a multistranded wire of closely packed thin strands.
For the example chosen, at low frequencies the bulk resistance of the copper wire causes a power loss of around 0·008dB. At 10kHz the loss rises to 0·009dB if the internal impedance were absent, and 0·016dB with the internal impedance taken into account. At 25kHz these values rise to 0·012dB and 0·028dB respectively. Hence the change in relative signal level from near-d.c. to 25kHz, with internal effects taken into account is around 0·020dB. This is quite a small change so it is not obvious that it would be noticed in a practical audio system.
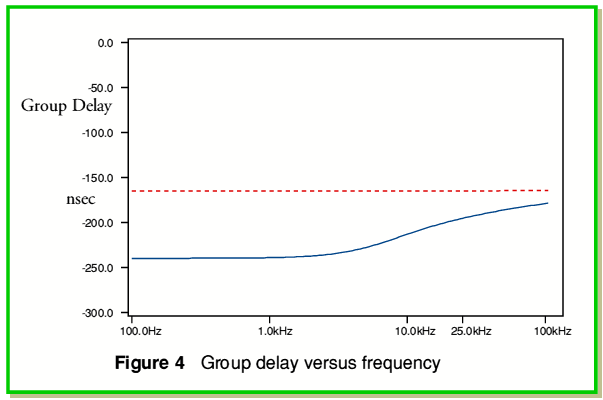
Figure 4 shows the group delay as a function of frequency. This measure is more convenient that plotting any change in phase since a propagation delay will manifest itself as a phase change that rises linearly with frequency. When signals have to propagate through a system the group delay is therefore a better indicator of any time domain effects that might alter the signal pattern. A uniform group delay value implies that all components will arrive with the same relationship as when they were transmitted.
As with figure 3, figure 4 shows two two lines, the solid (blue) one taking internal impedance into account, and the broken (red) line neglecting internal impedance. By examining these lines we can see that the internal impedance causes the group delay to depart from being uniform. If no ‘skin effect’ were present the group delay would be almost steady at 164 nanoseconds across the whole band plotted. However when the internal impedance of the wires are taken into account the group delay varies from around 240 nanoseconds at low frequency, to around 212 nanoseconds at 10kHz and around 195 nanoseconds at 25 kHz. The effect of the internal impedance is therefore to produce a differential group delay of around 50 nanoseconds across the audio band. Interestingly, high frequencies will tend to arrive slightly earlier than low frequencies.
Curiously, the above time delay values can be seen as ‘large’ or ‘small’ depending upon your starting point. To a microwave/RF engineer with experience of transmission lines a delay of around 200 nanoseconds seems oddly large for a twin feeder only three metres long. Since we are assuming that no magnetic materials are present and a twin feeder propagates a TEM wave we might expect a propagation velocity of
where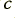 
is the velocity of light in vacuo, and 
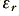is the relative permittivity. Here 
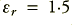so we would expect a velocity of around 2·44 × 108 m/s. Hence we might expect a propagation delay when using 3 metre cable of only around 12 - 13 nanoseconds. Yet we see values over ten times greater than this.
The reason for this discrepancy is that microwave/RF engineers usually arrange to match the source and load impedances to the cable’s characteristic impedance. This is far from being the case here. The load resistance is 8 Ohms, but the cable has a characteristic impedance of around 75 Ohms. Since the cable is also very ‘short’ in terms of the signal wavelengths it primarily acts as an inductor and resistor placed in series with the ‘low’ load impedance. At low frequencies the signal delay is therefore approximately equal to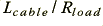 
which – ignoring internal effects – in the example equals around 164 nanoseconds. Hence the group delays we see are in broad agreement for what we would expect as a result of cable inductance in this example. The dashed line (equivalent to Litz wire) shows a value of 164 nanoseconds as internal inductance has been suppressed. This indicates that although the solid conductor (or a similar stranded wire) have a value of around 240 nanoseconds at low frequencies only around 80 nanoseconds of this is due to the wire’s internal inductance.
Despite the above, to an acoustic engineer the delays seem very small. Since sound propagates at a velocity of around 330 m/sec it will only travel around 16 microns in 50 nanoseconds. In effect, therefore, the above differential group delay is equivalent to a sound source that seems 16 microns nearer at high audible frequencies than at low audible frequencies. Again it is not clear that this would be noticeable in a practical situation.
