1. Skin Effect and cable impedance
There is a considerable amount of discussion (not to say argument!) amongst those interested in audio and Hi-Fi about the possible effects of cables upon ‘sound quality’. This tends to lead to some people adopting almost ‘theological’ viewpoints that differ fundamentally from the views held by others. One of the technical factors which is sometimes claimed to affect sound quality is what is usually called ‘Skin effect’.
In most electronics textbooks, the properties of cables and wires are considered as a form of transmission line. The text may mention briefly the skin effect without exploring this in detail. More often, however, the only parameters that tend to be considered are the capacitance per length, inductance per length, and their relationship with the signal’s nominal propagation velocity and the characteristic impedance of the system. The fact that normal materials have a finite conductance (or resistance) is not usually considered beyond its effect upon the d.c. (and low frequency) resistance of the cables and the resulting implied signal power losses.
In reality, when we transmit alternating signals along conductive lines we may experience effects due to what is generally called ‘skin effects’. This subject is widely misunderstood, and hence people occasionally tend to invoke this frequency dependent behaviour as the implied basis for all kinds of claims regarding the ‘sounds’ of different types of cables. The purpose of this analysis is to throw some light into this area and help provide some understanding of the effects of using conductors of finite conductivity.
In engineering textbooks, the consequences of finite conductivity and wire size are treated in terms of an ‘Internal Impedance’. This term is probably more useful that ‘skin effect’ as it acts as a reminder that the effects arise due to the fields internal to the conductor. The internal impedance per unit length of a wire is considered in Ramo et al. From this was may draw the following results as a starting point.
The d.c. (i.e. very low frequency) impedance of a wire which has a circular cross-section and is uniform may be said to consist of a resistance per unit length of
where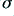 
is the bulk conductivity value appropriate for the material used to manufacture the wire, and 
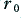is the radius of the wire. The resistance is in Ohms/metre if we are using S.I. units (which will be assumed from now on).
The wire will also exhibit an effective inductance per unit length at very low frequency due to its internal fields. At very low frequencies this has the value
where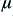 
is the permeability of the material. In general we can assume that this equals the value for free space
The detailed analysis in Ramo leads to the following expressions which can be used to determine the relevant wire resistance and inductance per unit length for a conductive wire of circular cross section at frequencies above d.c.
where
and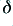 
is the ‘skin depth’ value which may be calculated via
where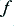 
is the signal frequency (as opposed to 
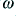the signal’s angular frequency).
In fact, using the above expressions we can show that
and specifying this factor in terms of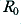 
and 
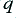may be more convenient when performing calculations.
Now,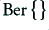 
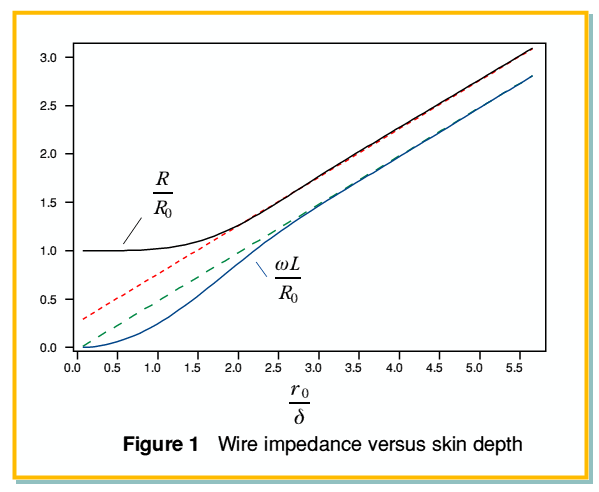
, etc are Bessel functions. We can find numerical expressions for evaluating these in a text like Abramowitz and Stegun. Using these we can compute values. For the sake of clarity is is useful to plot values normalised in terms of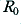 
. Some results of doing this are illustrated in figure 1. These are plotted versus 
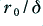so that the relevant nominal skin thickness is also normalised in terms of the wire radius. The solid lines plotted show the relevant values calculated from the above expressions.
Unfortunately, the expressions provided by A & S only cover the range for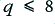 
which roughly corresponds to 
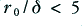. Above this value the Bessel functions become hard to evaluate and their combination tends to lead to a situation where a set of large values cancel to give a moderate result. Hence for computational simplicity we can use a simpler approximation for the situations where 
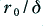is ‘large’. Here this may be defined as where this ratio has a value greater than 5.
The standard ‘h.f.’ approximation is that both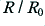 
and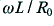 
will be essentially equal to 
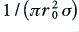. However by inspecting the results shown in figure 1 we can see that it is possible to do better than this and a more reliable approximation would be
This approximations are show in figure 1 by the broken lines. The approximation for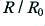 
is shown by a short-dashed red line, and that for 
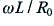by a longer-dashed green line. It can be seen that these approximations are likely to be reasonably accurate in the region 
.
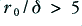2. Types of Wire
In general, electronic signals are conveyed using a ‘pair of wires’. These are used to form a closed loop (path) between the signal source and the load around which charge may flow. Broadly speaking we can then define a ‘cable’ to consist of a pair of wires. The most common forms of cable used in audio are ‘Twin Feeder’ and ‘Co-ax’. The basic properties of these are discussed elsewhere. Each of the wires may be a single, solid, length of conductor. More usually, however, each wire will consist of a bundle of conducting ‘strands’. Multistrand wires have properties which may differ from that of a single, solid wire of similar cross-section. We can therefore treat wires as falling into three general categories as outlined below.
- Solid core (i.e. just one strand of conductor per wire)
- Stranded wire (a bundle of thin strands of conductors)
- Litz wire (as stranded but with insulation between the individual strands)
For solid-core wires the above analysis can be used immediately to compute the internal impedance and deduce the effects it may have in a given situation. For the stranded and Litz wires we need to take the stranding and the effect of inter-strand contacts or insulation into account.
Litz wires consist of a bundle of very thin, individually insulated conductors. The insulation ensures that the current flows in all of the wires in the bundle as the charge cannot migrate towards the surface of the bundle. The entire cross section of conductor bundle is therefore used by the charge transport. Provided that the individual strands are thin enough, the strands all have individual radii that are small compared to the skin depth at audio frequencies. Hence the overall properties of the Litz bundle tends to be similar to that of a single wire of the same diameter of the bundle but where ‘skin effect’ is apparently absent.
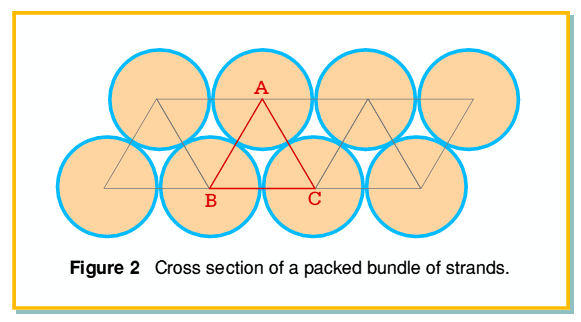
In practice, most of the multi-strand wires used for audio purposes have no insulation on the individual strands. This means they do not behave like a Litz wire. In stranded wires without insulation between the individual strands charge may cross from strand to strand. Hence current will tend to preferentially flow near the skin of the bundle of wires, just as it does with a single solid conductor of similar overall diameter. Hence when the strands are thin but in electrical contact with their neighbours we can expect the effect of internal impedance to be similar to that of a solid wire of a diameter similar to the bundle of strands. There is, however, one factor we should take into account. This arises when the strands do not ‘fill’ the bundle and their are air gaps. This is illustrated in figure 2. This shows a close-packed array of strands, each of radius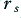 
.
Since the strands all have a circular cross-section we find that even if they are tightly packed into a hexagonal array there will be spaces in between the places where they touch. Hence a bundle of small packed strands that are in electrical contact can be regarded as similar to a solid but which has some air inclusions which mean that overall wire cross section is only partly filled with conductor. Given a value for the ‘fill factor’,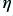 
, (the fraction of the cross section which is filled with conductor) we can treat the wire as being equivalent to a solid conductor of the same wire diameter, 
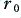, but having an effective conductivity of 
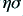. Thus the main electronic effect of using a bundle of strands is to dilute the effective conductivity and lower its apparent value.
To estimate the value of the fill factor we can note that the array has a symmetry similar to a packed array of equilateral triangles whose sides all have a length of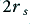 
. Taking one of these elemental triangles we can see that it contains three 60 degree sectors of conductor. Hence the cross sectional area of conductor in each triangle is equal to 
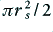. However the area of each triangle will be 
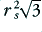. Hence the fill factor will be approximately equal to
Real strands will tend to deform slightly when compressed and may not have perfectly smooth, circular cross sections. They may also not be perfectly packed. Hence we can expect the actual value of the fill factor to vary accordingly in practice. In Litz bundles the insulation layers on the strands will also move the conductors apart by a small amount, thus reducing the fill factor value. Usually, we can expect this effect to be small as the layer of insulation is likely to be very thin. In most cases we can therefore tend to assume that the fill factor is reasonably close to unity so this is a reasonable assumption for general analysis. That said, in some specific cases we can take stranding into account by modifying the effective conductivity by an appropriate fill factor value.
