6.3 EH Fields and Domestic Waveguides.
In fact, we can now reveal that it is the electromagnetic fields that surround metal wires that actually carry the signal energy. Here we can examine three standard cases, starting with one that looks like the ‘house to house’ system we looked at earlier. In each case it turns out to be the product of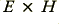 
that carries the power and the electrons are almost irrelevant except as a convenient place to ‘pin’ or ‘control’ the fields. The wires (more precisely, the electrons inside the wires) act to guide the fields, but it is the fields that do the real work!
In terms of electromagnetism, we can define the power flow in terms of the Poynting Vector
As a vector, this quantity has both a magnitude and a direction, so it in indicates both the rate of energy flow, and the direction in which the energy travels. To determine the total flow from one place to another we would need to integrate the value of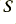 
over a suitable surface which is placed so that any path from place to place must pass through the surface. For wires, waveguides, etc, this usually means a plane surface perpendicular to the wires, located between the signal source and destination. We also should average the value over a suitable time (often one cycle of a periodic signal) to obtain a mean or average power value.
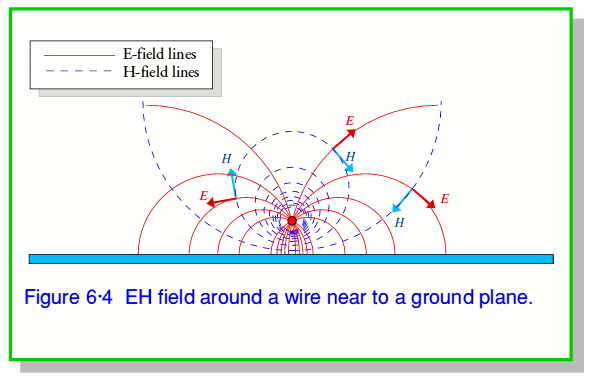
Figure 6·4 shows the E-field (solid lines) and H-field (broken lines) that are set up in the kind of arrangement considered in figures 6·1 and 6·2. Perhaps surprisingly, the ground tends to act as a fairly good conductor so far as the EH fields are concerned. Hence we usually obtain a pattern similar to that between a small wire and a flat conducting metal plane. (Which is often called a ‘ground plane’ for reasons that should now be obvious!) Since the metal is a good conductor, the E-field lines strike it normal to the surface, and the H-field at the surfaces is parallel to the surface. If we analyse the shapes in detail we discover the the field lines are actually all circles or arcs of circles.
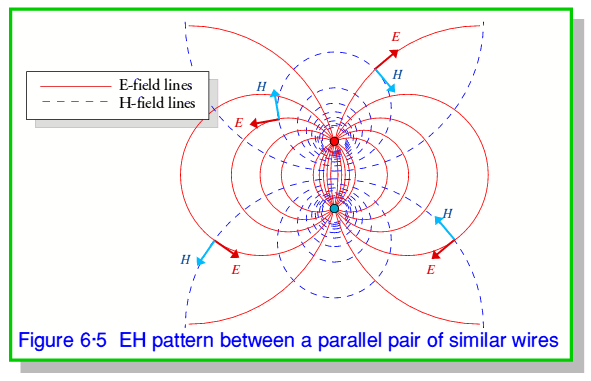
A good conductor acts like a ‘mirror’. We can therefore say that the fields we see above the ground behave just as if there was an image of this pattern below ground level. Of course, it only looks like this when we are above ground. However it leads to the related result shown in figure 6·5 which shows the field between a parallel pair of wires used as a ‘twin feeder’ to convey signal energy.
For the illustrations the top wire in each case is assumed to be given a positive potential w.r.t. the ground plane or lower wire. The current flow is assumed to be away from the observer in the top wire, and towards the observer in the ground plane or lower wire. This then gives the E-field and H-field directions indicated by the arrows on the diagrams. By the right-hand rule we can see that everywhere the Poynting Vector – and hence the energy flow – is away from the observer. If we reverse both the potentials and the currents (as would happen if the signal source reversed the polarity of the signal they are applying) both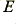 
and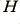 
would change signs. Hence the Poynting Vector’s sign would remain unchanged. The behaviour of the fields is therefore consistent with the currents and voltages we considered earlier. We can therefore use the Poynting Vector to show us the direction energy (and hence signal) flow.
If we ignore the ‘Earth’ wire, which is present (in the UK at least!) purely for safety reasons, normal house mains wiring is a form of twin feeder and acts essentially as a form of ‘waveguide’ to direct the electrical power from generating station, via National Grid, to the lights, TVs, etc, in our house. (In fact, at the risk of complicating things, long distance power transmission often uses three wires as this is more efficient, but we can ignore that here as being a detail.)
A pair of wires acting as a twin feeder is fairly cheap to make, and easy to use. It does, however suffer from two disadvantages. Firstly, the EH fields spread for some distance around the wires. As a consequence, any pieces of metal or dielectric near the wires will be in the field. Hence signal power may be lost by being coupled onto these objects, or the signal propagation behaviour altered by their presence. Secondly, at high frequencies the wires will tend to act like as an ‘antenna’ and may radiate some of the power rather than guiding it to the intended destination. To minimise these effects it is advisable to keep the spacing between the wires, and their diameters, as small as we can. It is also common to wind the wires around each other the wires together and make a ‘twisted pair’. Ideally we want to keep other objects much further away than the wire spacing, and keep the wire spacing much smaller than the free-space wavelength of the highest frequencies that we wish to carry along the wires.
Unfortunately, meeting the above requirements can be difficult at times. Also, thinner wires are likely to have a larger resistance, so will waste signal power heating up the wires. To overcome these problems it is common to use alternative forms of wiring or guiding. The topic of signals guides and fibres is a complex one, so here we will only briefly mention one widely used solution to the above problems – the Coaxial Cable. Often called ‘Co-ax’ .
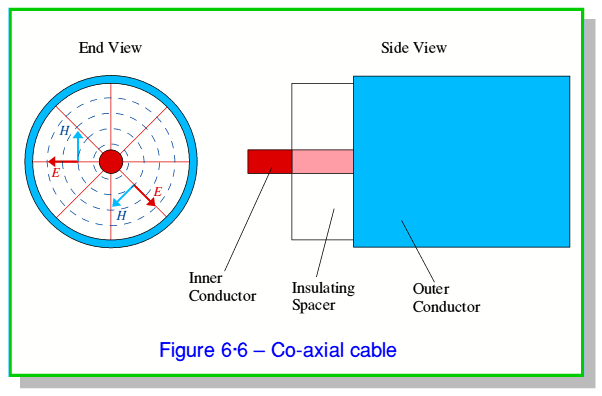
Coaxial Cable consists of two conductors, one of which surrounds the other. We can think of this as a variation on the wire-over-a-groundplane shown in figure 6·4. However we now bend the ground plane and ‘wrap it around’ the wire. The result is a wire inside a ‘tube’ of conductor with an insulating space in between. The two conductors usually have circular symmetry, and share the same long axis (hence the name). The space between them is also usually filled with a suitable dielectric material to keep the conductors apart and help the cable maintain its overall size and shape. The result has a typical form shown in figure 6·6. In this case the E-field is radial and the h-field is circumferential. As before, the power is carried by the EH fields. However unlike the previous examples, this field is now all ‘inside’ the cable. This means that the signal energy guided along the co-ax is unlikely to be affected by objects which come near to the outside of the cable.
The corollary of the above is that any unwanted signals (interference or noise) from elsewhere will now also be unlikely to inject itself onto the cables. Co-ax therefore falls into a general class of cables and guides which is said to be ‘shielded’. It efficiently guides the power from place to place, with little chance of any of the signal being affected by the cable’s surroundings. For this reason co-ax is particularly useful when we are dealing with low-power and/or high frequency signals. Hence it is used a great deal in radio systems and in sensitive measurement equipment. For similar reasons, many signal and radio cable connectors also have a co-axial form.
Summary
You should now understand the way in which wires and cables carry signals and signal energy in the form a an EH field pattern. You should also now know that although the charge carriers (free electrons) move in the conductors they only carry a tiny amount of energy, and move much slower than the actual signals. You should now be able to see the underlaying similarity of a wire over a return/ground plane, a pair of wires acting as a ‘twin feeder’, and a co-axial cable. The useful property of co-ax in keeping signals ‘shielded’ and preventing them from being lost should also be clear.
