6.2 Energy and Moving Electrons
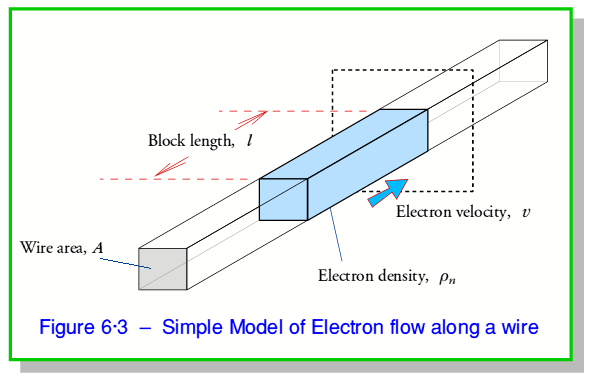
In the above we only took an interest in the voltage (potential difference) and the current. The simple ‘school textbook’ model of electricity tends to describe electricity as being similar to water flowing in a pipe. In fact this isn’t a very good way of looking at what is happening as it tends to hide some important features. To appreciate this, we can picture the electrons flowing along the wire as illustrated in figure 6·3.
Here we imagine the ‘free’ electrons that can provide the moving charges that constitute the current as having a uniform number density inside the material of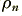 
electrons per unit volume. The current is the result of these moving along the wire at an average velocity, 
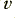. We can now define the current to be
where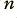 
is the number of electrons that cross a boundary cutting across the wire in a time, 
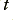, and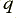 
is the charge per electron. By measuring the current in Amps, and the charge in Coulombs, we can say that 
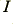Amps corresponds to 
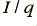electrons per second.
Since we know the density of the electrons in the wire we can turn this number into an effective volume of the electron distribution that will cross the boundary per second. This volume can be taken as a ‘block’ of the free charges which extends along a length,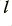 
, of the wire and covers its entire cross sectional area. Hence we can determine the length
Which implies that the free electrons are all tending on average to move this distance per second. Hence we find that the mean velocity of the moving electrons is
Lets now take an example of a copper wire with a square cross section of 1mm by 1mm. Avogadro’s Number tells us the number of atoms (or molecules) per gram-mol of the materal. The value of this number is 6·0225 × 1023. A ‘mol’ can be regarded as the atomic weight divided by the valancy value of the material. Copper has an atomic weight of 63·54, and a nominal valancy of one. We can therefore say that 63·54 grams of copper will contain 6·0225 × 1023 atoms, and each on contributes one free electron. Thus each gram of copper will contain 6·0225 × 1023/63·54 = 9·4783 × 1021 free electrons. The density of copper is 8·95 grams/cc. So the above is equivalent to saying that each cubic centimetre of copper will contain 8·4830 × 1022 free electrons per cc – i.e. in S.I. units we can say that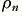 
= 8·4830 × 1028 per cubic metre. The wire’s area is 10-6 m2 so taking a current of one Amp for the sake of example, we can use expression 6.2 to calculate a mean electron velocity of just under 0·075 mm/second.
This result is an interesting one for two related reasons. Firstly, it is many orders of magnitude less than the speed of light in vacuum. Hence we can immediately see that it doesn’t correspond to the velocity of signals, or energy transfer, along metal cables. If it were simply the movement of the electrons that carried the signal we might have to wait a very long time indeed for a reply when speaking over a transatlantic telephone cable! A less obvious reason becomes apparent if we now work out the kinetic energy of the above ‘block’ of electrons. Each has a mass,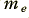 
, of the order of 9 × 10-31 Kg. So the kinetic energy passing the boundary per second will be
which, using the above values come to 1·5 × 10-20 Watts.
Now it must be remembered that the above calculations are only rough, hand-waving, estimates of the correct values. (For example, the effective mass of an electron will change when it is in a material.) However, this result shows that the rate at which the electrons move, and the amount of kinetic energy they carry, can be much smaller than we might expect. For example, it is common in domestic house wiring for a current of an Amp or so to support power levels of a few hundred Watts – i.e. many orders of magnitude greater than the value calculated above. We therefore have to conclude that the real burden of the signal and energy transfer is being carried elsewhere, and not simply by the electrons in the wires.
