From the explanation given above we can expect the simple PSU to provide an output d.c. level of around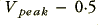 
Volts. To set a given voltage we must therefore be able to choose the amplitude of the input a.c. waveform delivered to the diode. This is the task of the transformer. To explain the detailed behaviour of a transformer is quite complicated. Here, for the sake of clarity, we can use a very basic model to explain its basic operation. Please note, however, that what follows is a rather simplified explanation and doesn’t really give the full picture. It is good enough for our current purposes, though.
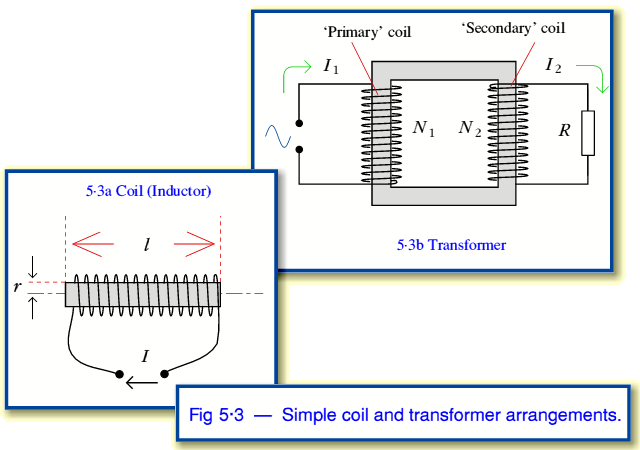
The basic properties of a transformer can be explained in terms of the behaviour of inductors. Figure 5·3a shows a coil of wire wound around a rod. Passing a current along the wire will produce a magnetic field through & around the coil. This current-field relationship works both ways — i.e. applying a magnetic field through the coil will produce a current. By looking at a good book on electromagnetics we can find the relationship
where
- B = field level at the centre of the coil (Teslas);
- I = current in coil (Amps);
-
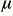= permeability of the rod (Henries/metre);
- N = number of turns of wire;
- r = radius of coil (metres);
- l = length of coil (metres)
The important feature of a transformer is that two (or more) coil windings are placed so that any magnetic field in one has to pass through the other. The simplest way to do this is to wind two coils onto one rod. However, this method isn't used much because it produces a lot of field outside the rod. This ‘stray’ field can cause problems to other parts of a circuit and may waste energy. Most modern transformers are wound on some kind of ‘ring’ of material as illustrated in figure 5·3b. This works as if we'd ‘bent around’ the rod & brought its ends together. The magnetic field is now coupled from coil to coil by the ring of magnetic material. It's conventional to call the coils on a transformer the primary (input) & secondary (output) windings. Consider now what happens if we apply an an a.c. current,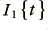 
, to the primary of the transformer shown in figure 5·3b. This winding has 
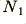windings, so it produces a magnetic field
where k is a constant whose value depends upon the size/shape/material of the transformer's ring. Since this field also passes through the secondary winding it must produce a current,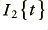 
, in the secondary, such that
putting these equations together we get
The transformer's output is connected to a resistive load. Since the current,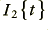 
, passes through this, the voltage across the resistor will be
The power dissipation in the resistor will therefore be
Now, from the principle of energy conservation, we can say that this power must be coming from somewhere! The only place it can come from in this system is the signal source which is driving the input current through the primary. Since we need to provide both volts & amps to transfer power this means that a voltage ,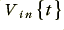 
, must be applied across the transformer's input (primary) terminals to set up the input current. The size of this voltage must be such that
We can now use equation 9 to replace the currents in this expression & obtain the result
This result is a very useful one. It means we can ‘step up’ or ‘step down’ the size of an alternating voltage by passing it through a transformer with an appropriate turns ratio,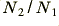 
. Note that when this is done the ratio of the input/output currents also changes by the 1/(same ratio). This is necessary as the transformer can't, itself, generate any electrical power. All it does is transform the power provided from the source. By choosing a suitable ratio, however, we can arrange for the required input a.c. voltage to drive the diode which then rectifies this to obtain the desired d.c. level.
