3·2 Order order!
Having established some of the general properties of filters, lets now look at some specific types and applications. Broadly speaking we can separate filters into Active versus Passive, As the names imply, an Active filter makes use of some gain device(s) as an integral part of the operation of the filter. Passive filters don’t actually require a gain device to work, but are usually accompanied by some form of amplifiers or buffers for convenience. Filters are also often referred to as ‘First Order’, ‘Second Order’, etc. This refers to the number of components (capacitors and inductors, not resistors or transistors) that affect the ‘steepness’ or ‘shape’ of the filter’s frequency response. To see what this means we can use a few examples.
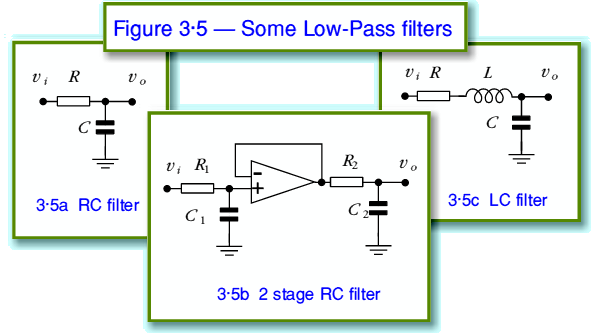
Figure 3·5 shows three simple types of low-pass filter. In each case we can use the standard methods of a.c. circuit analysis to work out the circuit’s voltage gain/loss,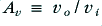 
, as a function of frequency and obtain the following results
In practice the above results would be modified by the impedances connected to the input and output of each filter, but the results shown are good enough our purposes here. We can in fact now re-write all of the above expressions in the general form
i.e. in each case the frequency response is given by an expression in the form of the inverse of a polynomial of some order,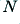 
. The relevant values for the three examples are as follows
| Filter
| order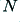 
| 
| 
| 
|
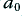
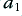
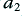
| 3·5a (simple RC)
| 1
| 1
| 
| -
|
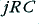
| 3·5b (two-stage RC)
| 2
| 1
| 
| 
|
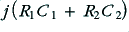
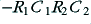
| 3·5c (LC)
| 2
| 1
| 
| 
|
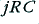
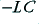
So 3·5a shows a ‘first order’ low-pass filter, but 3·5b and 3·5c are ‘second order’. In general, we can expect a filter of order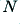 
to cause the value of 
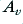to fall as 
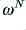when we are well into the frequency region where the filter is attenuating any signals (i.e. when 
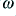is large for the low-pass examples). We can apply a similar general rule to other types of filter – high pass, etc – although very complex filters may require a more general expression of the form
3.3 Active filters, Normalisation, and Scaling
The above examples are all ‘passive’ filters. OK, the circuit shown in Figure 3·5b does use an amplifier (probably an IC op-amp) as a buffer between the two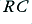 
stages, but this is just present to ensure that the two stages don’t interact in an unwanted manner. Active filters generally employ some form of feedback to alter or control the filter’s behaviour. This makes the designs more flexible in terms of allowing for a wider choice of shapes of frequency response, time-domain behaviour, etc. In theory we can make passive equivalents to most active filter so it may seem as the need for an amplifier is an unnecessary extra complexity. However the active filer offers some useful advantages. In particular, they help us avoid the need for ‘awkward’ components. For example, it is often good practice to avoid using inductors as these can pick up unwanted interference due to stray magnetic fields. Also, some passive filters may require large-value capacitors or inductors, which would be bulky and expensive. By using an active equivalent we can often ‘scale’ all the component values in order to be able to use smaller and cheaper components.
Most of the analysis and design of active filters is done in terms of Normalised circuits. To understand what this means, look again at the circuit shown in figure 3·5a. The way in which the filter’s voltage gain,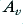 
, varies with frequency is set by the value of 
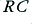. The important thing to note is that the behaviour isn’t determined by either 
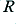or 
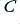taken independently. So, for example, if we were to make 
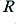ten times bigger, and 
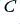ten times smaller, the behaviour would be unchanged. The 
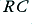value sets a ‘turn-over frequency’ we can define as
A Normalised version of the circuit would assume that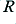 
was one Ohm, and 
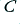was one Farad. This would set the turn-over frequency of 
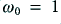Radians/sec (i.e. 
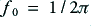Hz).
In reality, normalised values will be impractical, and we will usually want a specific turn-over frequency very different to the above value. However we can scale the normalised version of each circuit as follows:
- To shift the turn-over frequency to
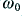we choose the 
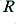and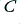 
values so that expressions 3.7 is correct
- To obtain convenient component values we then ‘trade off’ the values of
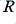and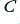 
against each other until we get something suitable. e.g. we may increase 
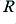by some factor, 
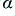, and then reduce 
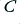by the same factor.
The choice of sensible values is a matter of practical experience so is hard to define on a webpage This is one of the areas of electronics where design is a skill, not a science which provides a uniquely correct answer. When using op-amps for the amplifiers in the active filer, we generally try to end up with resistor values in the range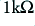 
to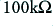 
, and capacitors in the range from 
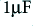down to 
.
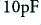Lets look at some examples of designs, then try scaling one for a specific result.
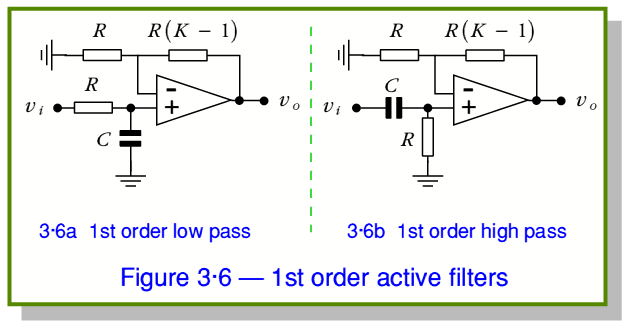
Figure 3·6 shows 1st order low and high pass active filters. For a Normalised version we would assume that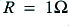 
and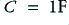 
. More generally we can say that the frequency response of 
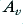for each of these will have the form
where we use a commonly used standard definition
Let’s now take as an example a real filter which we want to have a turn-over frequency of, say,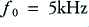 
. This means that in this case 
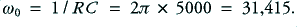If we try choosing a resistance value of 
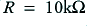this means we would need to choose 
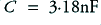to set the required turn-over frequency.
In the case of the above circuits the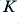 
value just sets the gain for frequencies well within the Passband of the filter. So we can choose 
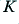to amplify the output by whatever amount is suitable for our purpose. (Although in practice it is usually advisable to choose a gain below ×100.) However for more complex higher-order filters the gain often alters the details of the frequency response, particularly around the chosen turn-over frequency. These effects can be seen in the following examples of second order filters.
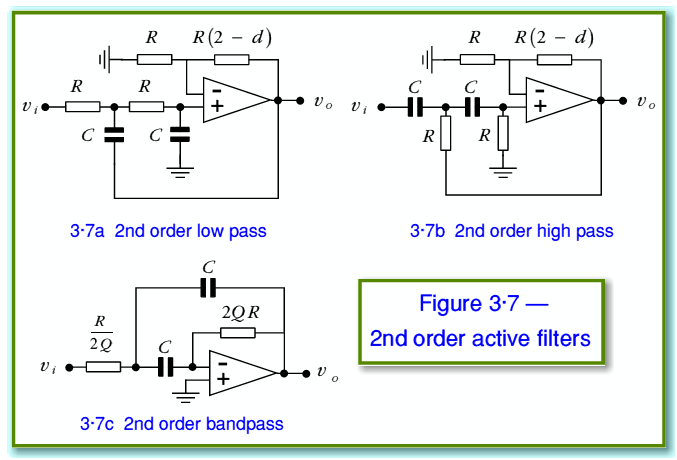
In this case an example of a band-pass filter is also included. The examples shown introduce two new quantities that have standard definitions. The Damping value,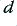 
, and the Quality factor,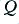 
The gain value,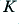 
is related to these via the expressions
The frequency response of each of the above is as follows:
The damping and quality factors have a very important effect upon the filter response. To see this we can start by take the damping factor’s effect on the high/low pass filters.
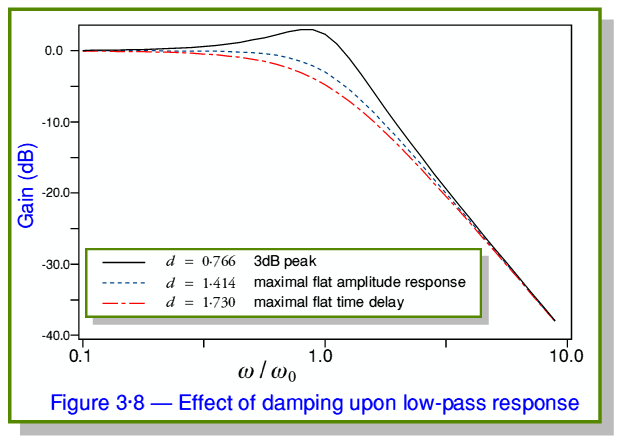
Figure 3·8 shows the relative frequency/amplitude response shapes for three possible choices for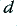 
. It can be seen that 
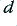values below unity produces a ‘peak’ in the response at frequencies around 
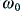. (In fact, if we were to reduce 
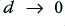the circuit becomes an oscillator and will oscillate at 
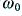.) Values of 
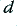greater than unity tend to ‘damp down the response and smooth out the corner at around 
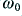. A choice of 
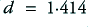(i.e. the square root of 2) produces a Maximally Flat Amplitude Response. i.e. the amplitude response covers the smallest possible range in the passband up to 
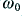. A choice of 
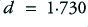produces a Maximally Flat Time Delay, i.e. the most uniform Group Delay in the passband up to 
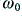. We can therefore in practice select a 
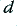value which suits best our purpose. Note that the gain in the passband also depends upon 
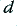. To make the changes in shape clearer the above graphs are normalised to a 0dB level of 
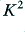. Note also that the above example uses the low-pass filter. The high-pass filter behaves in a similar manner but we would be referring to a passband that extends downward from high frequencies to 
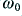instead of up to 
.
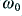The bandpass filter has a frequency response which has a width (to the -3dB points) of
and has a phase response that changes from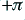 
radians at 
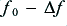to 
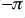at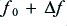 
. In effect, ‘Q’ sets the narrowness or sharpness of the bandpass filter. A sharper filter will allow us to pick out a wanted frequency from noise, etc, at other frequencies so a narrow filter is often desirable. This is why this variable is therefore often called the Quality Factor, and given the letter ‘Q’.
The filters used above as examples are just a few of the many types of filter that are available. Higher orders of filter can be made with many slight variations in the relative component values, and with various arrangements. The relative choices of component values (which then determine the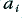 
and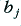 
coefficients in equation 3.6) determine what is called the Alignment of the filter and set its detailed response. The most common forms of alignment have names like Butterworth filters, Elliptic filters, etc. Each has its good and bad points but can be designed and analysed using the same methods as used above.
In practice it is common to build high order filters by cascading two or more lower order (1st or 2nd) order filters. This makes the system easier to design and means it can be less demanding to build. High order filters often require close-tolerance components with strange values which then have to be put together from series/parallel combinations of more usual values. There are also a number of specialist filters that use quite different techniques. The most common analog types are those based upon ‘biquad’ and ’NIC’ (Negative Impedance Convertor) arrangements. The NIC is particularly useful for special applications as it permits us to make a circuit which provides otherwise impossible values – e.g. a negative resistance or inductance.
At radio frequencies there are a number of special filters based upon the properties of some materials – Crystal Filters, Surface Acoustic Wave Filters, etc. And of course, these days, it is common to perform signal filtering in the digital domain, so there are a variety of digital filtering systems available. Since here we are concentrating on basic analog methods we won’t here examine how these work, but it is worth bearing them in mind for situations where they may prove more convenient than the analog filters described in detail here.
Summary
You should now understand how the behaviour a filter may be characterised by its Frequency Response (both in terms of amplitude gain/loss, and the way in which phase varies with the signal frequency). That this Frequency Domain behaviour also relates to a Time Domain behaviour. That it is often useful to define or use the Time Delay as a function of frequency to assess the filter’s effect upon signals. You should now also know that the Group Delay indicates the average time delay that signals encounter across the filter’s passband, and that a uniform Group Delay will avoid Dispersive distortions of the filtered signal.
You should now understand the concept of the Order of a filter, and know how to design simple 1st and 2nd order filters. That the Quality Factor or Damping of a filter affects the detailed response, and that these can be set by the component values selected. You should also now be aware that the Alignment of a filter can be chosen for optimal amplitude or phase or time properties in a given application, and that some ‘standard’ alignments with names like Butterworth Filters, etc, exist.
