One of the limitations which affect all real amplifiers is that they all have a finite Signal Bandwidth. This means that whatever amplifier we build or use, we find that there is always an upper limit to the range of sinewave frequencies it can amplify. This usually means that high frequencies signals won’t be boosted, and may attenuated instead. It also often means that high frequency signals may be Distorted – i.e. their waveshape may be changed. Some amplifiers also have a low-frequency limitation as well, and are unable to amplify frequencies below some lower limit. We therefore need to be aware of, and be able to assess, these effects to decide if a specific amplifier is suitable for a given task.
In addition to the above, there are many situations where we deliberately want to alter the signal frequencies a system will pass on or amplify. There are many situations where deliberate filtering is needed. Some common examples are:
- Low Pass Filters used to limit the bandwidth of a signal before Analog to Digital Conversion (digital sampling) to obey the Sampling Theorem
- Bandpass filters to select a chosen ‘narrowband’ signal and reject unwanted noise or interference at other frequencies.
- Bandreject filters used to ‘block’ interference at specific frequencies. e.g. to remove 50/100 Hz ‘hum’ (or 60/120 Hz if you happen to be in the USA!)
- ‘Tone Controls’ or ‘EQ’ (Equalisation) controls. These tend to be used to alter the overall tonal balance of sound signals, or correct for other unwanted frequency-dependent effects.
- ‘A.C.’ amplifiers that don’t amplify unwanted low frequencies or d.c. levels.
Here we will focus on some examples of filters, but bear in mind that similar effects can often arise in amplifiers.
3.1 Ways to characterise filters
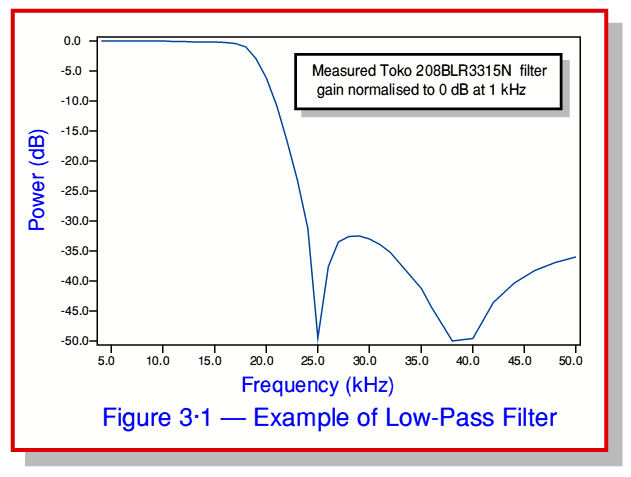
The most common and most obvious way to describe the effect of a filter is in terms of is Frequency Response. This defines the filter’s behaviour in terms of its Gain as a function of frequency. figure 3·1 shows a typical example.
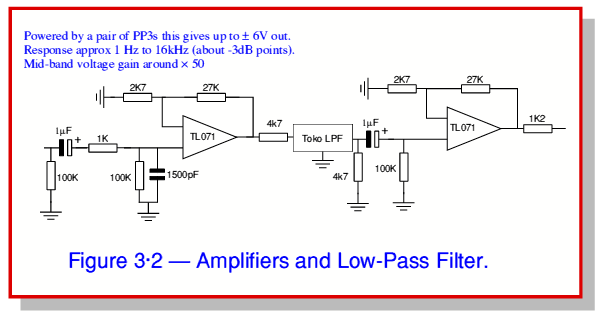
In this case Figure 3·1 shows the measured power gain (or loss!) as a function of frequency for a specific low-pass filter. This example is based upon a commercial audio filter sold under the ‘Toko’ brand name for use in hi-fi equipment. This filter is Passive – i.e. includes no gain devices, just passive components like resistors, capacitors, or inductors. As a result we need to counteract any unwanted losses in the filter. The overall circuit measured in this case is shown in figure 3·2.
Here the filter actually sits in between two amplifiers which raise the signal level. The filter’s job in the system this example is taken from is to stop high frequencies from reaching the output which is to be sampled by an ADC. The overall voltage gain is around ×50 at 1 kHz. The Toko filter passes signals from d.c. up to around 18 kHz but attenuates higher frequencies. Note also the pair of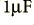 
capacitors in the signal path. These, taken in conjunction with the following 
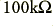resistors, act as High Pass filters to remove any d.c. as it this was unwanted in this case. The combination of the 
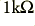resistor and 1500pF capacitor at the input also act as an additional low-pass filter.
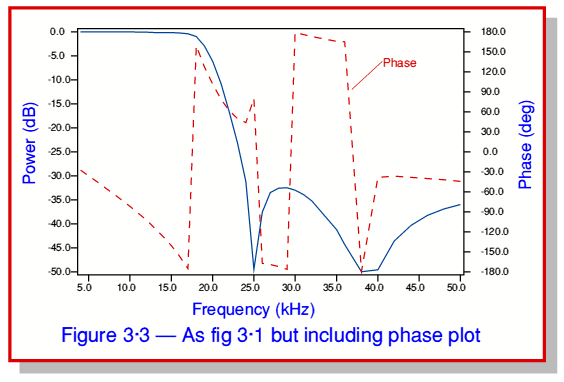
Although a frequency response of the kind shown in figure 3·1 is the most common way to display the behaviour of a filter, it doesn’t tell the whole story. When sinewave components pass through the filter they may also be delayed by an amount that depends upon their frequency. This effect is often represented in terms of a plot of the Phase Delay as a function of signal frequency. For the same filter as before the measured Phase Delay as a function of frequency is shown in figure 3·3.
In figure 3·3 the phase seems to ‘jump around’ in quite a complex way. However the underlying behaviour is simpler than it appears. There are two reasons for this. Firstly, the phase measurements are always in the range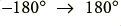 
, but the actual signal delay may be more than a half-cycle. When making phase measurements we can’t normally distinguish a delay of, say, 50 degrees, from 360 + 50 = 410 degrees, or any other multiple number of cycles plus 50 degrees. If we look at the phase plot shown in figure 3·3 the phase seems to ‘jump’ from 
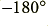to about 
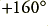at around 16 kHz. In fact, what has happened is that the real signal delay has increased from 
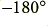to around 
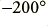. However, since the measurement system only gives results in the limited range it assumes that this is the same as 
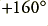. Despite the apparent hopping around, the actual signal phase delay tends to increase fairly steadily with frequency. The second reason for the complex plot is that at some points the signal level becomes very small. e.g. in figure 3·3 at around 25kHz. When we try to make a phase measurement on a tiny signal the result becomes unreliable due to measurement errors and noise. Hence the value at such a frequency can’t be taken as being as reliable as at other frequencies.
Measured plots of phase delay versus frequency therefore have to be interpreted with some care. That said, the phase behaviour is important as we require it along with the amplitude behaviour to determine how complex signals may be altered by passing through the filter. In practice, though, it is often more convenient to measure or specify the filter’s time-effects in terms of a time delay rather than a phase. We can say that a phase delay of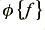 
(radians) at a frequency 
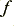is equivalent to a time delay of
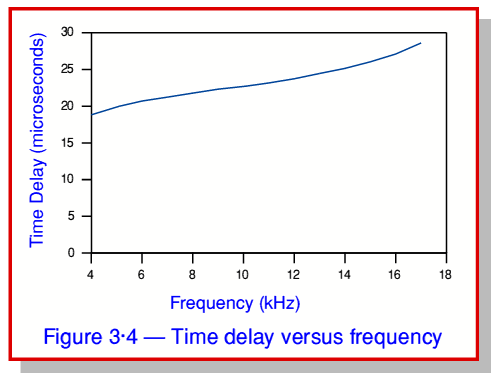
Figure 3·4 shows the time delay as a function of frequency for the same filter as used for the earlier figures.
Looking at figure 3·4, we can see that when expressed in terms of a time, the delay seems rather more uniform and does not vary as quickly with frequency as does the phase. This behaviour is quite common in filters. In effect, the filter tends to delay signals in its Passband by a fairly uniform amount. However since a given time delay looks like a phase delay that increases linearly with frequency, this behaviour isn’t obvious from phase/frequency plots. The term Group Delay is used to refer to the average time delay imposed over the range of frequencies the filter is designed to pass through. In this case we can see that for our example filter the Group Delay value is around 22 microseconds. The term comes from considering a ‘group’ of signal frequencies.
In fact, we can always expect signals to take a finite time to propagate through any circuit or element in a system. Hence we can also quote Group Delay values for amplifiers, transistors, or even cables. Unless the delay is so long as to make us wait an annoyingly long time for a signal, a uniform Group Delay is normally fine as it just means we have to allow a short time for the signal to arrive but its waveform shape is unaffected. A non-uniform delay will mean that – even if the amplitudes of frequency components remain relatively unchanged – the signal waveform will be distorted. Hence in most cases we try to obtain filters and other elements that have a uniform delay. That said, there are situations where we require a Dispersive element – i.e. one which delays differing frequencies by differing times. Some forms of filter are actually designed to be All Pass. i.e. they don’t set out to alter the relative amplitudes of the frequency components in the signals, but are designed to alter the relative times/phases of the components.
Although we won’t consider it in detail here, it should be clear from the above that we can model the behaviour of filters just as well by using their Temporal Response to waveforms like short pulses or ‘steps’ (abrupt changes in level) as by using sinewave methods. In fact, the two ways of understanding the signal processing behaviour are linked via Fourier Transformation. We can therefore characterise amplifiers, filters, etc, in either the Time Domain or the Frequency Domain as we wish. When dealing with continuous waveforms the frequency domain is usually more convenient, but when dealing with pulses the time domain is more useful.
