

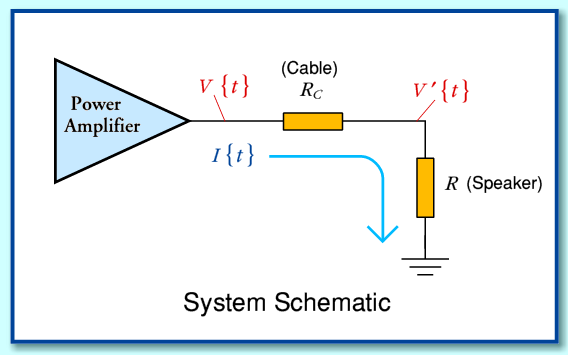
| The currents and the resistance are normalized, so the peak woof and tweet currents are 1, and the resistance of the wire is also normalized to 1. The woof current is the blue line, the diss is (Asquared) I2R, so as you can see, it peaks at 1, and is always positive (real dissipation cannot be negative). It is your basic sine squared waveform, a direct result of the woof current flowing through a wire by itself. Note that for an ideal load, this is also exactly the same dissipation time profile scaled differently. The tweet current is the magenta line, called Bsquared. again, I squared R... With biwiring, the total wire dissipation is of course, the sum of the two, A squared plus B squared, and the load dissipation at the speakers is an exact scale of the wire dissipation. The yellow line (asq plus b sq) is the summation of the wire loss in biwiring. Now, consider both signals travelling in one wire, such as monowiring.. The equation is P = I2R, with I = A + B (A+B)2 = A2 + B2 + 2AB. So, subbing A + B for I creates 3 parts of the power dissipation, the third and most interesting component being the 2AB part.. I put that on the graph, that is the brown (I think) color. Note two very important things about the 2AB component... 1. It goes NEGATIVE!! At first blush, that seems impossible..However, look at it's value compared to the yellow line which is the A2 + B2 part....note that if you sum them, they NEVER go negative. In other words, the 2AB component is a modulation of the expected dissipation. So, the monowire dissipation never goes negative.. 2. It is a ZERO INTEGRAL power waveform...in other words, what is below zero is exactly the same area as that above zero. Since FFT algorithms cannot spot a zero integral power waveform, it isn't seen. Think of the instant in time when the woof has 1 ampere positive and the tweet has one ampere negative...at that instant, a monowire sees zero current, therefore zero power loss within the wire... But, a biwire setup has one ampere in the bass wire with it's dissipation, the tweet wire has negative one ampere and the exact same loss as the bass wire... The result? In a monowire setup, the current of one signal will modulate the losses that are caused by the other..when I see loop resistance recommendations at the 5% level, I cringe.. |
| ‘ideal’ | 0 | 0 | ||||
| ‘real’ |
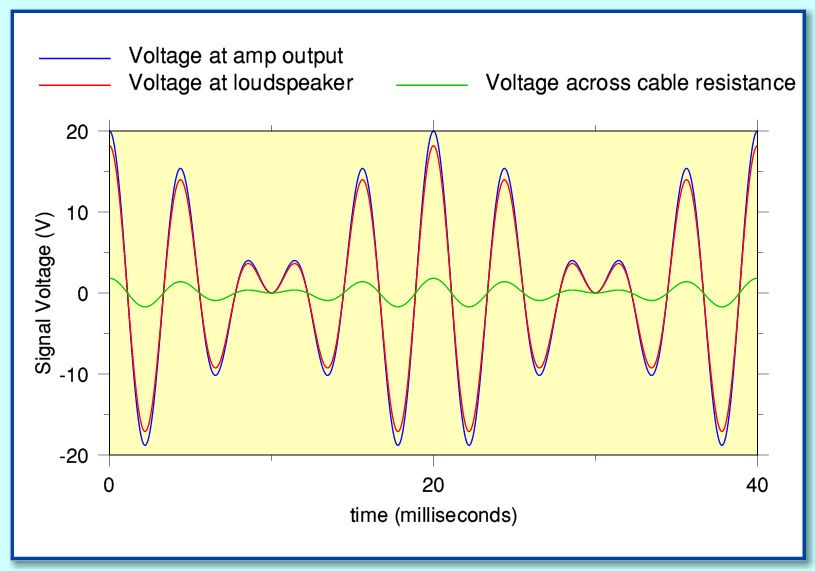
| ..that 2AB product I detailed, is the product of two frequencies, so there are frequencies produced that are not the fundamentals... |
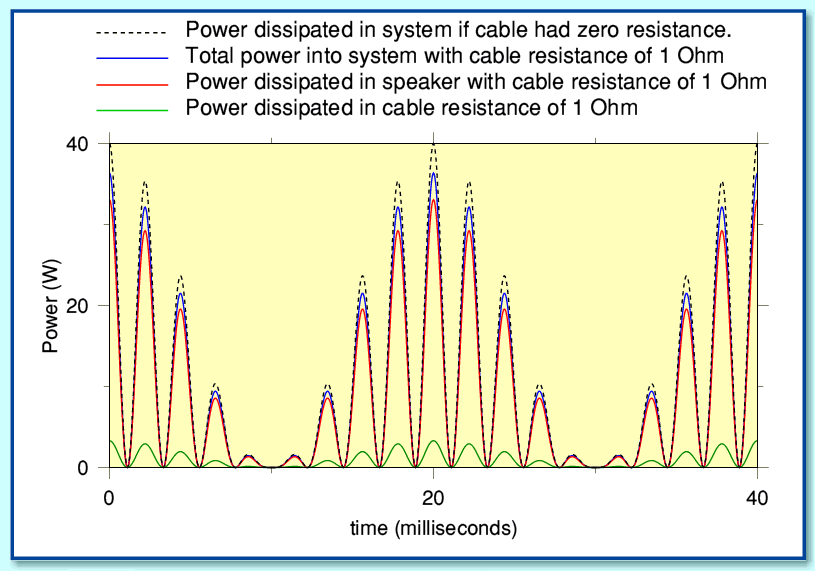
| [snip] The woof current is the blue line, the diss is (Asquared) I2R, so as you can see, it peaks at 1, and is always positive (real dissipation cannot be negative). [snip] The tweet current is the magenta line, called Bsquared. again, I squared R... With biwiring, the total wire dissipation is of course, the sum of the two, A squared plus B squared, and the load dissipation at the speakers is an exact scale of the wire dissipation. The yellow line (asq plus b sq) is the summation of the wire loss in biwiring. Now, consider both signals travelling in one wire, such as monowiring.. The equation is P = I2R, with I = A + B (A+B)2 = A2 + B2 + 2AB. So, subbing A + B for I creates 3 parts of the power dissipation, the third and most interesting component being the 2AB part.. [snip] |