“Bi-wiring” is a controversial topic. Some people are quite certain it makes an audible difference. Some others are convinced that it can’t actually make any difference at all. The purpose of this analysis is to try and decide whether it is at least theoretically feasible that bi-wiring can make any difference.
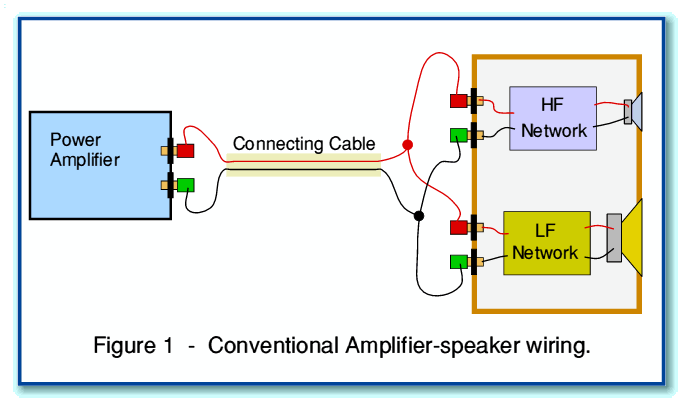
To define what is meant by “bi-wiring”, and understand what effects it may (or may not) have, we can start by considering the situation illustrated in Figure 1.
This shows an amplifier connected to a loudspeaker by a standard cable made from a pair of connecting wires. For clarity, only one channel of a stereo pair is shown. The loudspeaker consists of two drive units. – a high-frequency (HF) unit often called a “tweeter”, and a low frequency (LF) unit often called a “woofer”. Loudspeakers generally employ a “cross-over network” to direct low signal frequencies to the woofer, and high frequencies to the tweeter. In the example shown here this network is split into distinct HF and LF sections. This split permits the loudspeaker to be bi-wired. (Not all loudspeaker cross-over arrangements will permit this without modification.) In practice, as shown here, loudspeakers designed to permit bi-wiring have extra sets of input terminals which may be joined together when bi-wiring is not employed.
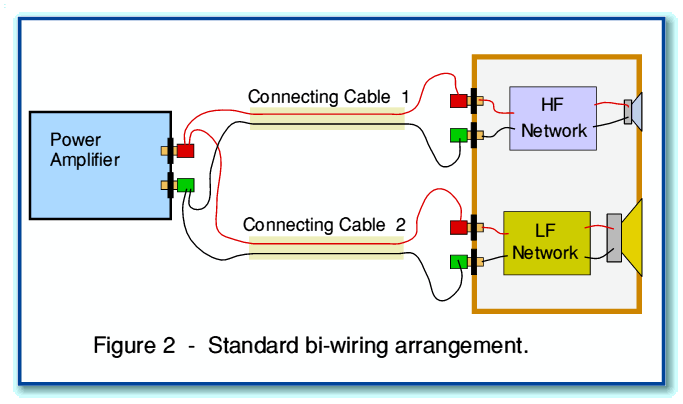
In the conventional wiring arrangement shown in Figure 1, the HF and LF input terminals are wired together in parallel at the speaker, and just one pair of connecting wires are employed to link both speaker units to the amplifier. In most cases “bi-wiring” means using an extra pair of connecting wires (i.e. another cable) so that the signals for the tweeter and woofer are sent from the amplifier to the speaker by separate routes. This bi-wiring arrangement is illustrated in Figure 2. In this new arrangement, Cable 1 carries the signals destined for the tweeter, and Cable 2 carries the signals destined for the woofer.
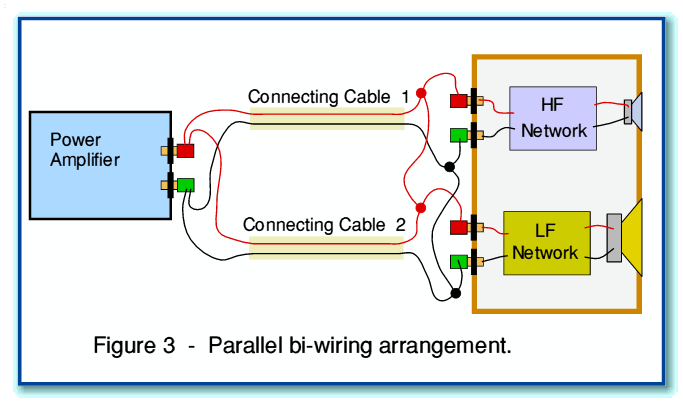
Various arguments have been presented for this bi-wiring arrangement by adherents who feel it alters the sound. For example, it may be claimed that each of the two cables may now be optimised in some way for the limited range of signal frequencies it now carries, and hence act more effectively. Alternatively, it is sometimes claimed that separating the signals for the tweeter and woofer means they do not now ‘interfere’ in some manner which may arise when they share the same cable. Unfortunately, these claims are generally unclear in technical terms, and there is a general lack of any reliable analysis or measured data to support the claims. This makes it questionable whether the claims are justified. It is also unclear whether the alternative arrangement in Figure 3 might also be “better” than the conventional arrangement. The arrangement in Figure 3 is also bi-wired, but the pairs of wires are now joined at both ends of the signal connection from amplifier to loudspeaker.
In the modified arrangement shown in Figure 3 both cables are used “in parallel” to connect signals to both speaker units. The question now becomes, “Are the arrangements shown in Figures 1, 2, and 3, all going to produce exactly the same results in use?”
Detailed analysis of the three arrangements is made difficult by two factors. Firstly, the electrical properties of the items involved can be quite complicated. The networks used in loudspeaker crossovers may contain a number of components and have a complex behaviour. Similarly for the actual speaker units. As we have seen on the webpages on cables, even the behaviour of simple twin-feed connecting cable can be more complicated that we might expect.
The second problem for a precise analysis is that the actual details of the loudspeaker crossover, etc, will vary a great deal from one model of loudspeaker to another. Hence we can expect any results to depend upon the choice of loudspeaker, cable, etc.
To make understanding these questions easier we can address a simpler question – i.e. we can ask, “Is is possible for the changes between the arrangements in Figures 1 - 3 to make any difference, or not?” To answer this question we need only look at a simplified example. If, in that example, a difference can be show to be possible, then it implies that a difference may appear even in more complicated arrangements. If no such difference is shown, this does not necessarily resolve the real issue, but at least we have progressed part of the way to a better understanding. With the above in mind we can now form a electronic models of the above arrangements, simplify them as far as seems reasonable, then compare their computed behaviours.