Previous articles on sound have all been based on processing information in Linear Pulse Code Modulation (LPCM) form. This represents the waveforms as a series of binary numbers. For example, pairs of 16-bit values taken at 44.1 ksamples/sec for use on Audio CD. However it is now common for people to communicate or store sound in the form of ‘mp3’ files. I recently experimented for the first time with these, and encountered some results I didn’t expect...
MP3 files essentially store the sound information as a series of groups of values that define the waveform spectra during a series of time periods covered by each ‘frame’ of data. This allows a set of rules to be use to ‘thin out’ the data by removing information about spectral components which are judged to be unnecessary. The process is analogous with the JPEG/JFIF system used for photographic images. The idea being to discard information whose absence has no noticable effect when the remaining data is used to recreate an image or sound.
This kind of process suffers from two snags. Firstly, that the quality of the results depends on how good the ‘judgement rules’ are. Secondly, that if we remove too much data the results will suffer from easily noticeable degradation. However many people seem quite happy with MP3 files compressed down to data rates of 128 kb/sec. (This compares with 1,411 kb/sec for Audio CD standard LPCM. The obvious advantage is that the user can have many more ‘tunes’ on a portable music player or computer hard drive, and the files can be downloaded more quickly.
Personally, I don’t have much interest in pop music, or having a portable music player. So I’ve not been drawn to using mp3 - until recently when I learned that the Royal Concertgebouw Orchestra were issuing, free, a set of symphonies as downloadable mp3 files. Unlike most pop tunes, these were made available at a bitrate of 320 kb/sec. The high bitrate should mean that many of the details a 128 kb/sec mps would discard would be preserved, so the results should sound pretty good. I therefore decided to download the symphonies and give them a try.
I don’t own a portable mp3 or ‘media’ player. But I do have some machines that can play mp3 files if they are on a CD. So I used CDBurn to put copies of the files onto a disc. The Audio Cd player I currently prefer is a Rega Apollo, and also this plays mp3 files. Listening to this it was clear that the player was producing excellent results, and I found the symphonies thoroughly enjoyable. However I decided that I’d like to be able to divide each symphony into tracks to make access to individual movements easier. I also felt that having the recordings in the form of Audio CDs would be more convenient as I could then use them on players that can’t understand mp3.
Since I own a couple of Pioneer audio CD recorders I connected one of these to the spdif (digital) output of the Apollo. I then played each mp3 in turn whilst running the recorder. This produced Audio CD format versions of the recordings which I edited with Trackmaker and then wrote back onto CDRs. Since I was recording a digital stream and the mp3 files were made at CD sampling rate, these recordings represent the sequences of LPCM values generated by the Rega from the mp3 data. However whilst doing this I started to wonder about how my ‘hardware’ route (Player connected to recorder) would compare with using software to generate a LPCM file from each mp3. This is where the surprises started...
To generate LPCM files using my Iyonix I downloaded the application !MP3toWAV which has been produced by Roger Darlington. This makes use of the well-known and well-regarded LAME mp3 program. This ran on my machine at about x 0.6 speed. i.e. to took about 10 mins to convert each 6 mins of audio, and produced a WAV format output. I then converted this into my standard data file format for LPCM. I then had two LPCM versions of the mp3 original. Now, in theory the mp3 data unambiguously defines the waveform pattern it represents. So the ‘Rega’ (hardware conversion) and ‘Lame’ (software conversion) routes should have given me identical files when fed with the same mp3. A snag here was that the hardware recordings required me to start the recorder running before I started the player. So each Rega conversion produced an LPCM file with a long stream of samples whose value equalled zero. This meant I had to analyse the data and compare their patterns so as to be able to time-align them correctly. I will say more about that process in another article as it involves some interesting ways to examine sound data. Here I want to focus on the actual results once I was able to correctly align the two versions of the LPCM data.
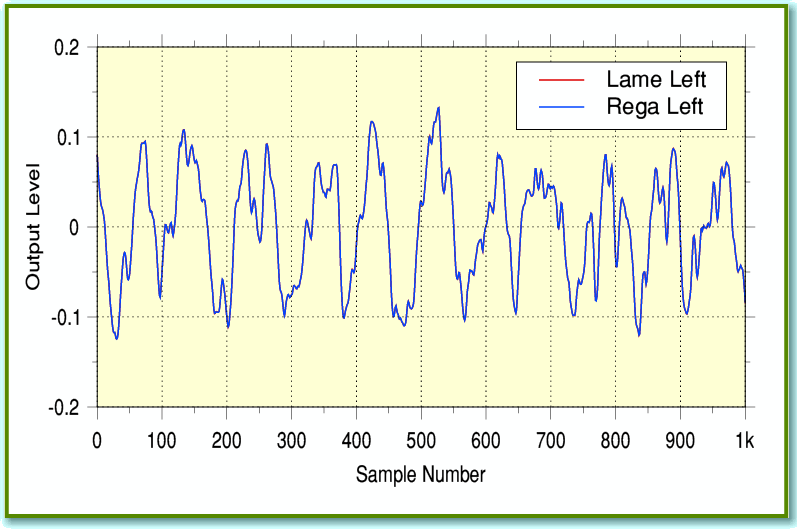
Figure 1
Figure 1 shows a section from each of the LPCM results. The output level shown is scaled so that the maximum possible CD values (+/- 32768) would output +/-1. Although it looks like only one line is plotted there are actually two waveforms. It is just that they are so similar that one sits on top of the other and hides it from view! For clarity I’ve just shown the left-channel waveform for the Lame and Rega conversions. Looking at Figure 1 you might think the two waveforms are identical, and that there is no problem. But now examine Figure 2.
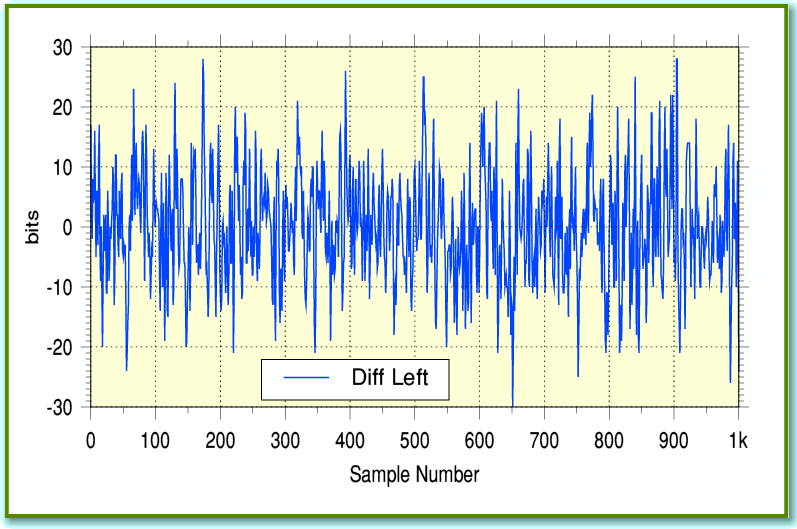
Figure 2
This shows the difference between the Rega and Lame values for each left-channel sample during the same section as for Figure 1. You can see that the values generally differ by up to over 20 bits. Since the signal waveforms have an amplitude of around +/-0.2 (i.e.. 0.2 x 32768 = 6552 bits) the discrepancy is of the order of 20/6500 = 0.3%. This is too small to be easily visible in Figure 1. But for audio fans it is worrying. The implication is that (at least!) one of the conversion methods is introducing some kind of error or distortion at the level of a few tenths of a percent. This may well be audible. Alas, the situation may be even worse than this. Look at Figure 3.
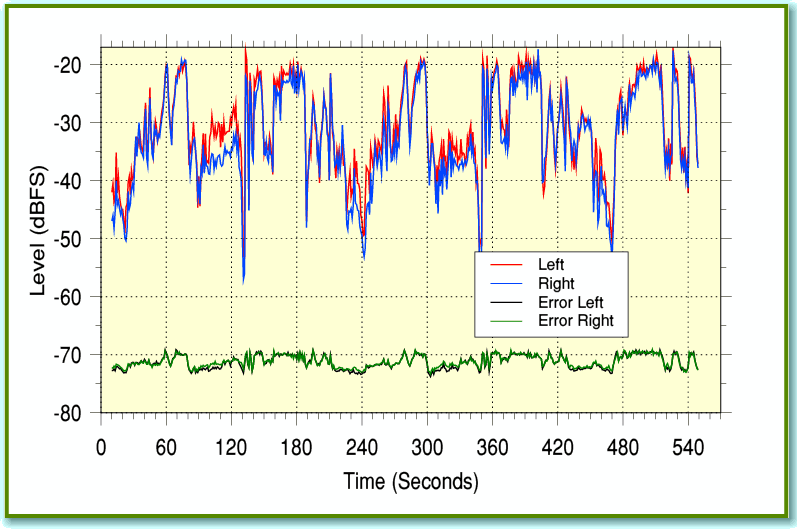
Figure 3
The upper two lines show the power level during a series of 1 second chunks of the symphony. These show the power level of the music varying over the range from about -20dBFS down to just over -60dBFS. The lower two lines hover around -70dB. These show the error (i.e. the difference between the Rega and Lame versions). What is particularly alarming is that this error doesn’t vary much as the signal power goes up and down. This means that when the music is only playing softly (i.e. approaching -60dB) the error level is only about 15dB below this. So rather more than a few tenths of a percent at such times!
Translating the above into waveform amplitudes in binary values we can say that 0dBFS corresponds to levels of the order of +/-30000. This roughly means -20dBFS corresponds to +/-3000, and -70dBFS corresponds to +/-10. This implies that whatever the intended signal size, the least significant three or four bits of each sample value are being destroyed. The implication is that at least one of the conversion methods only has a resolution of around 12 or 13 bits per sample. Not the 16 bits per sample we expect for CD Audio.
In principle - in the absence of any processing or computation errors – both of the two methods really should be able to give identical results to the full 16 bit level. The error (difference) should be zero. It is a concern that this isn’t the case in practice. So I will continue to investigate and report on progress in later articles if I can.
6th Nov 2008
Jim Lesurf
1350 Words