In the last ‘sound’ article I outlined the idea that we can use Fourier Transformation as the basis for being able to reduce the unwanted background noises that sometimes accompany recordings. However I also warned there are some snags...
Figure 1
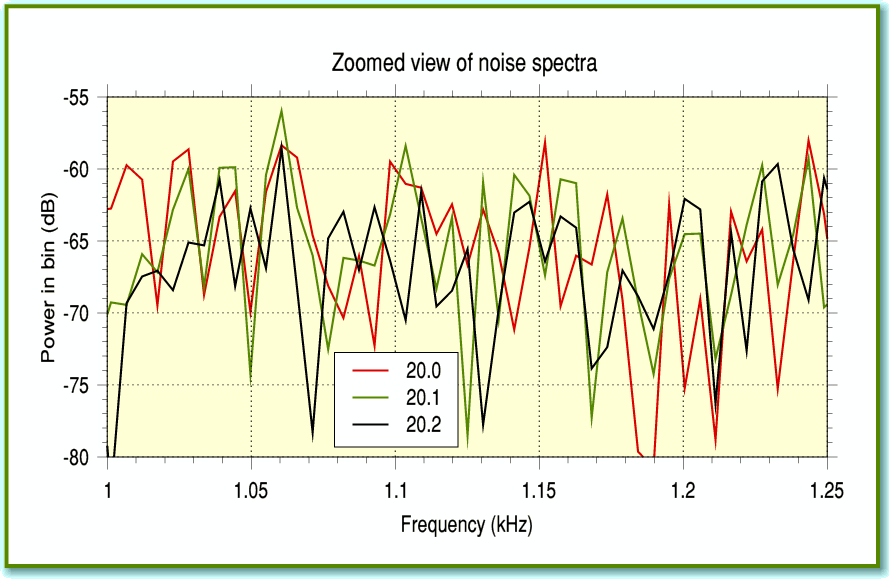
Figure 1 illustrates one of the main problems we have to deal with. It shows the same frequency range section for three spectra. In each case I took a chunk from a recording of random noise, and used !TrackFFT to obtain the spectrum. The only difference was that each chunk is from a different timed chunk, beginning at 20, 20.1, and 20.2 seconds from the start of the recording. For clarity I’ve just plotted one channel of some stereo noise for the three chosen time chunks, and only shown a narrow frequency range.
On average, the noise power at each frequency is somewhere around -65 dB relative to the maximum level. But since noise is random, we see that the actual value changes unpredictably from one frequency to another, and from one time-chunk of the recording to another. You can see that the actual values vary over a range of more than 10dB.
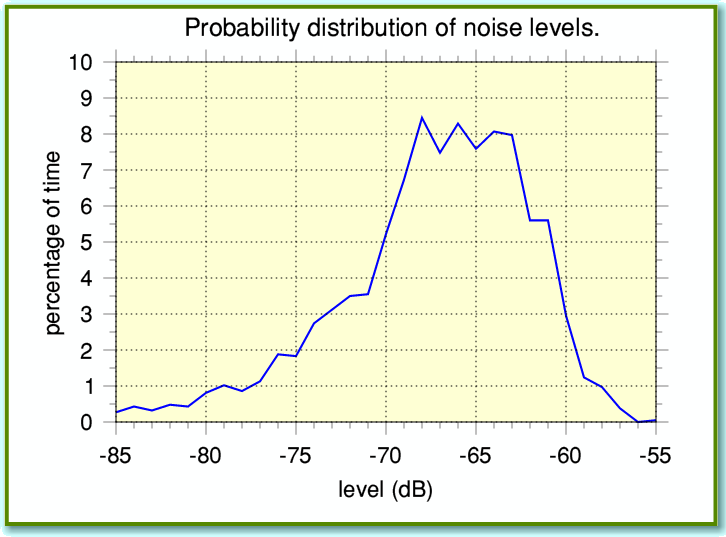
This variability was one of the reasons why I produced the application !TrackFFTScan, which allows the user to do FFTs of a series of time-chunks and get averaged results for the signal power level as a function of frequency. We can assess this behaviour by taking a number of FFTs of different time chunks of the noise, and working out how often we get various power levels at a given frequency. Figure 2 shows an example of this, using the same noise recording. Here I divided the results into 1dB ‘bins’ for statistical purposes, and then plotted what percentage of the results gave a given level. You can see that most of the time the level was in the range between about -60 dB and -70 dB. But some of the time the noise level falls well outside that range.
Now the question I am leading up to is, “What ‘cut off’ level should we set, below which we decide a spectral component is ‘noise’ and can be suppressed?” Recall that the aim is to set any noise components to zero whilst leaving any wanted signal components alone. This is to ‘clean up’ the spectrum before it is used to produce a new version of the signal with the noise removed.
Figure 2
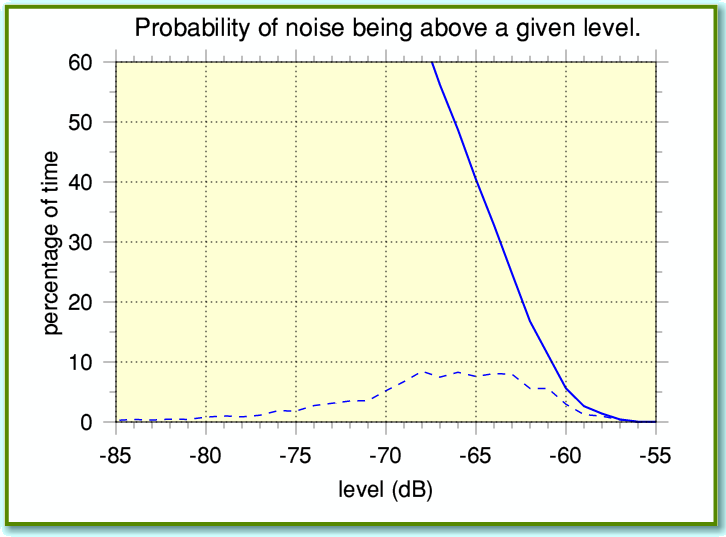
Looking at Figures 1 and 2 we can see that simply using the average noise level for our decision won’t work a lot of the time as the noise is often louder than this average. The result would be that much of the noise would remain. So we need to choose a higher value. Another way of assessing this is illustrated in Figure 3.
Figure 3
This shows a cumulative result. The solid line shows what percentage of the time the noise was above a given level. (The broken line repeats the same pattern as Figure 2 so you can compare the two shapes.) Looking at this we can see that if we’d chosen, say, -65 dB as our cut-off value then we’d have found that the noise was louder than this around 40% of the time. The result would be that we’d only suppress about 60% of the noise power. This would only reduce the total noise by about 4 dB. Noticeable, but the result would probably still be audibly noisy.
If we wanted to suppress more like 90% of the noise – to drop the total background noise by about 10dB – we’d have to choose a cut off level around -61dB. To get a noise suppression of 20dB (99%) we’d have to increase this to more like -58 dB.
In itself, that is fine. But the problem is that as we are tempted to ‘raise the bar’ to exclude more of the noise, we also tend to catch more signal components that happen to be at a low power level. Hence we can easily end up suppressing signal details – or at times the entire signal! This isn’t a problem if the signal is much louder than the noise. But if it is, then we may not need to have to worry about noise suppression in the first place! So in practice we may have to make a judgement about what levels to choose. To make things more complicated, the noise level may well vary with frequency, and be different for the left and right channels of a stereo recording. The noise level may also wander up and down with time, or alter its spectrum, etc, in some way. So what may at first look like a simple task turns out to have hidden pitfalls.
The FFTs I use in !TrackFFT and !TrackFFTscan take chunks of the recorded data that are 8192 samples (per channel) in length. Since CD Audio data is sampled at 44,100 samples/sec (per channel) this means each sampled chunk is 185 milliseconds in duration. The resulting spectra have a frequency resolution of 1/0.185 = 5.38 Hz. An obviously sensible question at this point is therefore, “Would it help if we chose to use longer (or shorter) chunks?”...
One effect of choosing a different length for each FFT is that the frequency resolution and number of frequencies in the spectrum change. If we decided to quadruple the length of the FFT to 32,368 samples (per channel) we’d end up with four times as many frequency components in the spectrum. One interesting consequence of this is as follows.
Consider a case where the unwanted noise level is ‘white’ and has a total power of, say, -60 dB relative to the maximum possible. When we say noise is white we mean its spectrum has – on average – a uniform spectral power density. i.e. that the power level is spread equally across all the frequencies in the allocated bandwidth (22.05 kHz for CD Audio). This total power is the same regardless how many samples we chose to take for a chunk to FFT. So the noise power added up across all components in the 32,468 sample spectrum is the same, on average, as for an 8,192 sample one. But there are four times as many spectral components in the 32,468 sample spectrum. This means that the average noise power at each individual frequency component will be lower by a factor of four. The result is that the noise power level in the spectrum tends to fall if we increase the number of samples (signal duration) taken and transformed.
The above result is a very significant one in Information Theory and Measurement terms. Alas, it is also widely misunderstood, particularly some audio ‘reviewers’ who use FFTs analysers in consumer magazines! It does look like a way to help us distinguish unwanted noise from wanted signal by increasing the difference in their levels when we take a spectrum. But I’ll stop there for now to give you a chance to decide if it will help in practice with our aim of cleaning up audio signals ...or not...
Jim Lesurf
1200 Words
18th Jun 2008