Making sense of supertweeters.
Recently, there has a been a growth in interest in “supertweeters” – speakers designed to be able to reproduce sounds at frequencies well above the frequency range normally regarded as ‘audible’. Typical examples of these are the add-on units manufactured by Tannoy, which can reproduce frequencies up to over 50 kHz. Some listeners are convinced that using these has a subtle audible effect and improves the sound. Others argue that we simply can’t hear frequencies much above 20 kHz, so supertweeters cannot possibly have any effect. The result is an argument which has yet to be resolved.
Here I’d like to suggest a simple explanation for why the output from supertweeters may well have an audible effect, but without actually requiring us to be able to hear above 20 kHz.
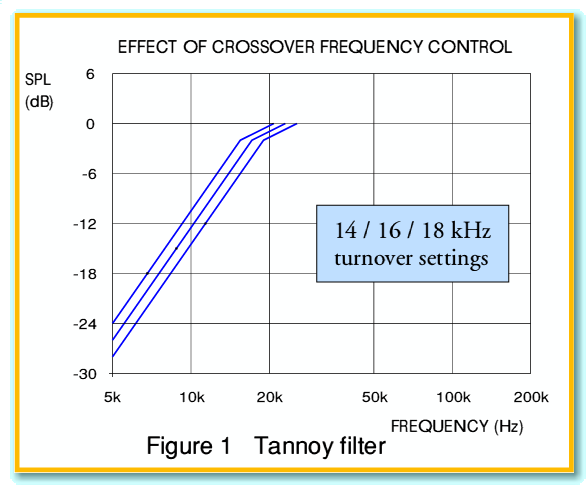
To understand the possible explanation we can start with the above graphs in figure 1, taken from a document which Tannoy have made available on the web. This shows the nominal crossover behaviour for their ST50 range of supertweeters, for three choices of turnover frequency – 14 kHz, 16 kHz, and 18 kHz. The document that contains the original of the above also states that the filters used are 3rd order.
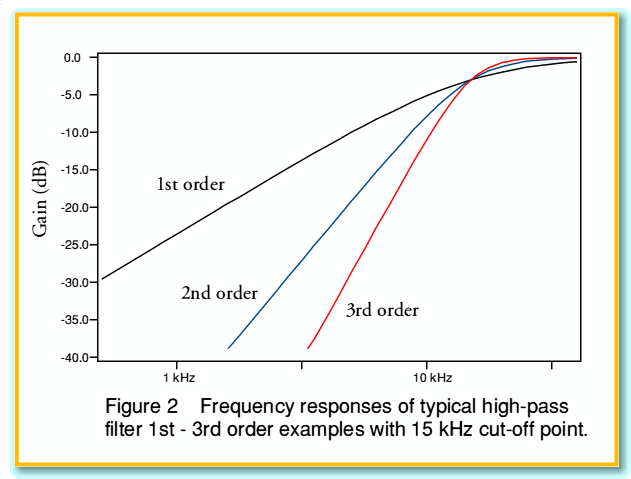
The relevance of the order of the chosen filter can be seen by considering figure 2. Here, for the sake of illustration, three filter shapes have been chosen, each with their -3 dB turnover points at 15 kHz. It can be seen that as we increase the order of the filter the amount of low frequency that will ‘leak’ thought can be reduced. Once we are well below the turnover frequency we can expect a first order filter to reduce the output by about 6 dB each time we have the signal frequency, but a third order filter will reduce the output by around 18 dB each time we halve the signal frequency.
One the above basis we might expect the output from a filter like this (and hence the supertweeter connected to it) to be negligible when we are well below the turnover frequency – especially when using a third (or higher!) order filter. Looking at the Tannoy filter it would seem that the output can be expected to be reduced by around 20 dB (i.e. a factor of 100) in power by the time we are at frequencies around 5 kHz. This may seem small enough to neglect, however we need to take coherence into account.
The supetweeter and the main loudspeaker whose output it is intended to enhance are driven by the same initial signal waveform. This means the outputs from the supertweeter and main speaker have a specific relationship. Relationships of this kind are called coherence. In situations like this, when we combine the contributions we must add their amplitudes (not simply the powers), taking any relevant phase or time delays into account.
The significance of this can be illustrated by an example. Let’s consider what happens at the frequency where the supertweeter is radiating a signal which is 10 dB down on that radiated by the main loudspeaker. If we simply add the powers this means we would expect a combined result which is 10 percent greater as a result of the supertweeter contribution. i.e. a rise of around 0·4 dB. Where the signals are coherently related we now need to combine the amplitudes. A factor of - 10 dB (0·1) in power corresponds to a factor 0·31 in amplitude. Thus if we happened to be in a situation where the signals were perfectly in phase, the resulting combined amplitude would be 1 + 0·31 = 1·31 rather than 1·00 when we add in the supertweeter contribution. Since the power scales with the sqaure of the amplitude this represents a rise of over 70 percent in the power (2·3 dB). Hence we might sometimes find a rise of over 2 dB in the signal level as a result of adding in an extra -10 dB contribution from a supertweeter. This is distinctly larger than the 0·4 dB we would get with incoherent power combination of unrelated signals.
Now in practice, the situation is generally far more complex than the above assumes. In general, the contributions are not perfectly time-aligned or in phase. Where the phases differ, the result does not usually add up to such a large total. Indeed, in some circumstances the main loudspeaker and supertweeter contributions may subtract. In these circumstances a -10 dB supertweeter contribution would change the total amplitude to 1 - 0·31 of the level the main speaker alone produces. In this situation the combined power will change by -3dB – i.e. the power level will be halved by the effect of the -10dB contribution from the supertweeter.
The precise time/phase relationship will depend upon the details of the speakers used, the positions of the speakers and listener in the listening room, reflections from the surroundings, and the frequency. Overall, if we average over a range of frequencies and locations the result tends to come out as if we had incoherently added the powers of the main speaker and the supertweeter. However in a specific listening position, at each frequency, the signal level (and its phase) will be determined by a coherent addition. As a consequence, the frequency response may be changed by much more than we might expect by the addition of a supertweeter. In addition, these changes might occur at much lower frequencies than the nominal turnover frequency below which it may seem as if the supertweeter is having no effect. The result may be quite marked, and audible, alterations in the overall frequency response below 20 kHz despite the supertweeter only radiating relatively modest power levels in this frequency range.
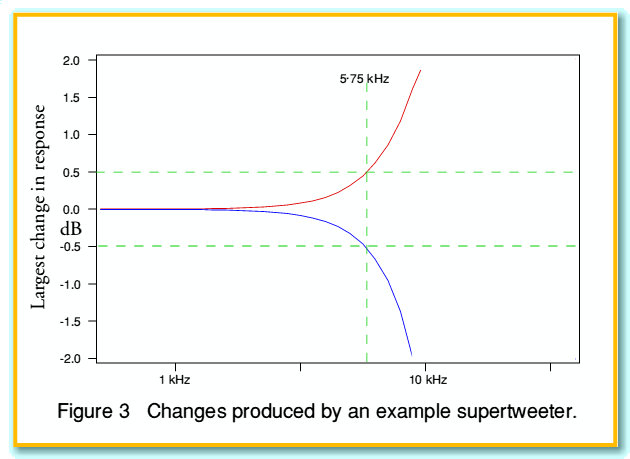
For the sake of illustration we can make some simplifying assumptions. Firstly, we will assume ‘perfect’ loudspeakers. The main speaker is assumed to have a flat response up to 20 kHz. The supertweeter’s actual output power is assumed to follow the third order response curve with its turnover point at 15 kHz, and have an output level above this that matches that of the main speaker at lower frequencies. We then ignore any room reflections or the effects of any objects in the room.
Under these assumptions, figure 3 illustrates the range of possible alterations in the signal level which may occur when we connect the supertweeter into the system. The red line shows the greatest rise (obtained when the main and supertweeter contributions happen to add perfectly in phase), and the blue line the largest drop (when they happen to oppose in phase). Looking at these curves, we can see that variations of the order of a plus or minus 2dB or more can be expected in the region around 10 kHz and above.
The above graph should not be taken to indicate the actual change in response in any specific case. The actual response would usually be much more complex than the above. It does, however give a sort of ‘envelope’ within which typical responses will tend to appear.
If the argument presented here is correct, then a supertweeter may have an audible effect because its use alters the response at frequencies well below 20 kHz. This may be the case even when the supertweeter is designed to have an output that is largely confined to higher frequencies. To test this possibility some relevant measurements would be required. However it looks as if supertweeters may be audible, even for listeners who can’t hear anything about 20 kHz, or when listening to musical signals that contain no energy above 20 kHz. This may explain why people say they can hear the effect of supertweeters, even using CD music sources which should have no components about 22 kHz.
Jim Lesurf
21st April 2003