Filters for bi-amping speakers
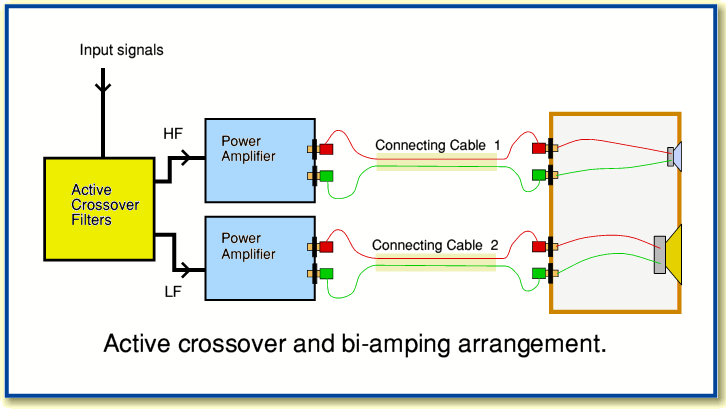
Many of the loudspeakers used in domestic audio systems employ two speaker units - one for the low frequencies, the other for the high frequencies. As a result, the speakers often contain a set of filters which tend to be called a ‘crossover network’ whose task is to pass the low frequency components to one unit and the high frequency components to the other. In most systems these networks are passive and are built into the speaker. However some users have an interest in a ‘bi-amping’ arrangement where the low and high components are divided before being sent to a pair of power amplifiers, and the outputs of the power amplifiers then sent to the individual units. This arrangement is illustrated in the diagram shown below.
This filtered bi-amping arrangement has the potential advantage that we can avoid passive components in the parts of the system that have to carry high powers and currents. It also means we can connect each speaker unit directly to the output of an amplifier. It debatable, however, that this inevitably leads to improved results as there are various considerations which a simple change from a passive arrangement to a split bi-amp one may not take into account. However for what follows I will ignore any complications and simply concentrate on the design of active filters that may be useful for an active crossover system to be used as part of a bi-amping arrangement.
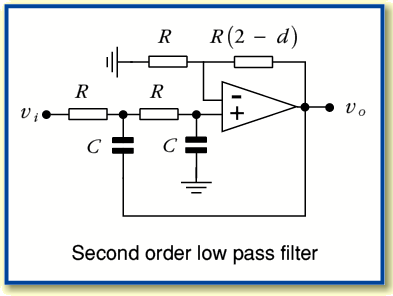
For the sake of example, here I will examine the use of 4th order filters, and build these by combining 2nd order arrangements. The basic building block of a 2nd order low-pass filter is shown in the diagram below.
The design equations can be taken from various standard texts. Here I will refer to the Active Filter Cookbook by Don Lancaster. (Sams ISBN 0 672 21168 8).
The nominal turn over frequency,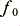 
, can be used to determine the value of 
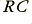via
If we use for our example a turn-over of 1 kHz and choose a nominal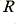 
value of 10 k
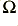this leads to a value of 
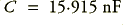. The shape of the filter response and its LF gain are determined by the choice of the damping factor value, 
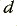. For a 2nd order maximal flatness shape we should choose d = 1·414. This means that
The LF (voltage) gain will be
The overall gain of the 2nd order filter is, in general, given by the expression
where
are the standard notations for expressions of this kind.
The above allows us to define a standard 2nd order maximal flatness LP filter, choose circuit values, and compute its response.
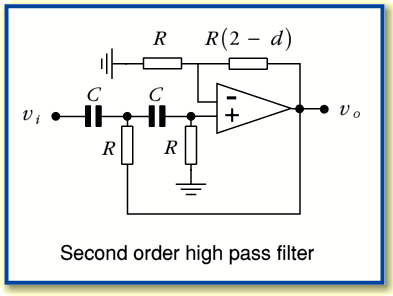
The equivalent 2nd order high-pass filter would have an arrangement as shown in the diagram below.
With the same notations and definitions as before we can say that the response of this will be given by
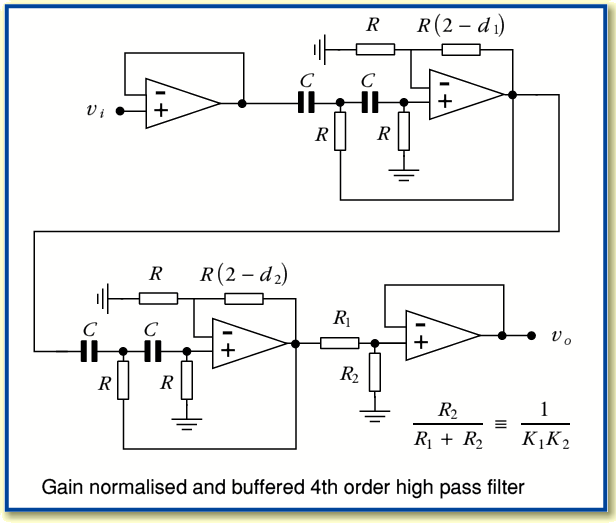
We can now construct a 4th order filter by using a cascade of two 2nd order filters. The diagram below shows an example of this and represents a 4th order high-pass filter. To make a 4th order low-pass filter simply employ two 2nd order low-pass building blocks in a similar way.
In addition to the two 2nd order stages this circuit now includes input and output buffer stages and also gain normalisation. The resistor pair,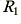 
and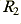 
, are used to correct the high-frequency gain back to unity. The diagram also indicates that the two 2nd order sections may have different damping values (and hence different gains). From Lancaster we find that to make a maximal flatness 4th order arrangement constructed in this way we should choose values of 
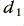= 1·848 and 
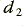= 0·765 which leads to low frequency gain values for the two stages of 
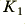= 1·152 and 
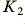= 2·235. This would lead to an overall high-frequency gain of 2·57 unless corrected with the resistor pair.
In this case if we choose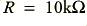 
and a turn over frequency of 1 kHz, then we should use the same 
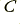value as for the 2nd order example, but the gain resistor values will be
For other frequency values than 1 kHz simply scale the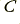 
and/or 
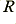values to ensure that the product 
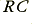value is in accord with
Page 1 of 2
