Critique of Loudspeaker cable webpage
Many manufacturers of ‘high quality’ domestic audio cables make claims for the audible performance of their cables. In some cases they put forwards a ‘scientific’ argument in support of their claims. Alas, as yet, I have not found any of the arguments to be plausible for various reasons. This does not necessarily mean they cables do not “sound good”. For all I know, they may be excellent. However my concern here is to cast a critical eye over the ‘scientific’ arguments they make. For the purpose of example I will here focus on what is on a specific page
http://www.analysis-plus.com/Pages/report981.htm
which is presented by a company called “Analysis Plus” to try and support their claims.
In general, their argument seems to be that their cables are audibly superior due to adopting an hollow oval cross-section to mitigate effects due to “skin effect” and “bunching”. (Internal impedance effects.) Before proceeding to a detailed consideration of their argument and claims, it may therefore be worthwhile to make some general points.
The first point is that it is doubtful that internal impedance has any audible effects in conventional well designed audio cables. It is true that these effects tend to cause the wire/cable impedance to rise with signal frequency. It is also true that this may well occur in the audio band with many cables. However the effects are quite small. So small, indeed, that it is doubtful they would normally produce an audible effect.
These effects are considered in detail on the pages on cables in the “Analog and Audio” section of the Scots Guide to Electronics. Anyone who wishes to see a more general analysis may therefore find those pages of interest. However here we can consider a specific example for the purpose of illustration. The example chosen is a simple co-axial cable, 2·5 metres long. The inner conductor is taken to have a radius of 0·5mm, and the outer conductor has an inner face radius of 2·3mm. The assumed thickness for the outer conductor is 0·2mm. The conductor is assumed to be fairly ordinary copper. The dielectric is assumed to be an air/PTFE mix with an epsilon of 1·5. These values are consistent with the examples on the “Scots Guide” and seem reasonable for a fairly modest type of co-axial cable. The characteristic impedance of the cable is approximately 75
The cable is assumed to be driven by a 600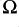
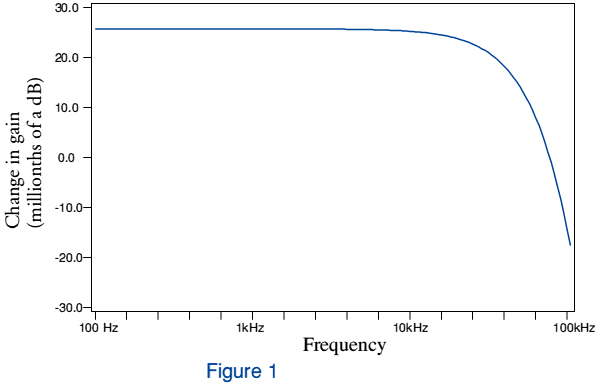
source and the load impedance is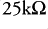 
. Figure 1 shows how the gain response of the cable will be affected by internal impedance. The value plotted is the change in gain we get between an ‘ideal cable’ (that has no resistance whatsoever, and no internal impedance) and a real cable which has the resistance and internal impedance behaviour we expect for copper conductors as specified above.
Note the vertical scale is in millionths of decibels. Across most of the audio band, taking internal impedance into effect causes the gain of the source-cable-load combination to change by around 25 millionths of a decibel. It seems reasonable to say that this is a very small change! If I calculate correctly, it corresponds to a change in the signal voltage level of the order of 3 parts per million.
Some other points may be worth noting here. Firstly, that to a large extent the change in gain is fairly uniform over the frequency band up to around 20kHz. In fact this change is mostly determined by the real ‘d.c.’ resistance of the cables. If we had permitted the ‘ideal’ cable we are comparing with a ‘real’ one to have normal resistance the result would have the same shape as shown above, but would have been displaced vertically so the low-frequency section was at a value of around 0 millionths of a decibel.
In practice an overall change in gain of around 25 millionths of a decibel is very unlikely to be noticed. A frequency-dependent change in gain is more likely to be noticeable. However for the above example, this is much smaller. If we compare the gain values at low frequency and at around 20kHz we can see they only differ by around 5 millionths of a decibel. Hence we can expect that suppressing internal impedance will only alter the frequency response across the audio band by this level. It is perhaps also worth noting that for the example a 2·5m length of co-ax was assumed. When using 1m of cable, the effect would be noticeable smaller!
Now although it seems implausible, it might be that tiny changes of this order are audible. However if so, we have some awkward questions to deal with. For example, as has been considered in a recent issue of Hi-Fi News, we can expect the transmission response of the air to vary with temperature, humidity, etc. Hence we can expect comparable or larger changes to occur randomly as we listen. These would tend to swamp any perceivable differences due to cable internal impedance. Also, if our ears are this sensitive, we would continually be aware of these moment-to-moment changes, produced by central heating, our breathing out warm moist air, etc.
Another factor to be born in mind is that the frequency response imperfections of other items of equipment are likely to be much greater than the above, and may also vary with conditions.
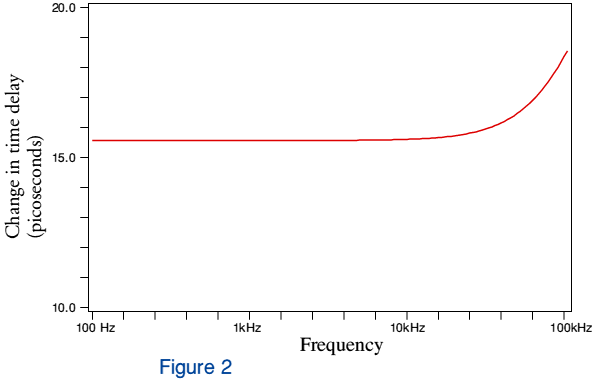
Figure 2 shows the change in time delay, plotted as a function of frequency, between our ‘ideal’ cable and one that has resistance and internal impedance. Note that here the units are in picoseconds. To get a feel for this timescale we can note that a soundwave in air would propagate approximately 3·5 nanometres in 10 picoseconds. Hence for this to be audible implies we would also be able to shift a loudspeaker unit position by a few nanometres, and hear the resulting change. This seems implausible.
From the above example we can see that the actual effects of internal impedance can be very small indeed. So small, in fact, as to make it doubtful that we would normally be able to sense an audible effect. Although here we have considered co-axial interconnect as an example we obtain similar results when considering ‘twin feed’ (i.e. a pair of wires) as loudspeaker cables. This subject is considered in more detail on the Scots Guide. There it is indicated that for Twin feeder used as loudspeaker cable, the effects of internal impedance may be higher than in the above example. This is mainly due to the much lower load impedance (order of 4 - 8 Ohms) rather than the change from co-ax to twin feed.
However even in loudspeaker cable, the effects of internal impedance should usually be quite small. A typical case shown on the Scots Guide pages indicates changes of the order of a few hundredths of decibels from from low frequency to 25kHz, even for cables that have not had their conductor diameters and spacings well chosen. It remains uncertain whether people can reliably hear frequency response changes of the order of 0·02dB or less. And even if they can, it seems unlikely to be worth regarding as a large change in audible terms. The effect can, of course, largely be suppressed by Litz construction if desired. So even if these small effects are felt to be deleterious, then can be avoided without having to resort to novel or expensive cable geometries.
Another general point which may be worth considering is as follows: “If a manufacturer believes that internal impedance is the factor that affects audible performance, why do they seek to invent novel cable arrangements when Litz wire is available?” Litz wire consists of multiple, individually insulated, strands. By using Litz construction we can effectively suppress internal impedance effects at audio frequencies. So why not use it?
One can only speculate as to the reason for the above. However one possible answer that may apply in some cases is that a manufacturer may wish to use a ‘proprietary’ arrangement which they can use as a “Unique Selling Point” when selling their cables. This is similar to the way toothpaste manufacturers continually come up with “new ingredients”. If people can be satisfied that the novel and proprietary arrangement is a good one, then the manufacturer can then also use intellectual property rights to inhibit any competitors from making an equivalent. This does not mean that their ideas are “bad”, just that this approach is commercially more viable than a commonly available solution.
Having dealt with the situation in general terms I can now move on to consider some of the detailed statements on the Analaysis Plus page. The general results presented above should now make it easier to understand the real implications of what they write. Much of what they write is reasonable, but nevertheless, the implications the reader is left to draw may not be relevant or appropriate for audio cables. In what follows I will put quotes from their page in italics to indicate that they are quotes.
Near the start of the page they write:
“Unfortunately, cylindrical cable designs have a number of serious drawbacks, including current bunching, skin effect phenomenon, and frequency effects that lower the performance of the cable.”
Given the analysis I have presented earlier it is somewhat doubtful to claim “serious drawbacks” here, since the effects are probably so small as to make it dubious that they would be audible. In addition, this problem will affect any geometry to some degree, and would be most simply dealt with by Litz construction without then any need for a change in geometry.
“Skin effect describes a condition in which, due to the magnetic fields produced by current following through a conductor, the current tends to concentrate near the conductor surface...”
Since they indicate that they have expert knowledge of this topic I assume they are aware that this statement is not quite correct. Internal impedance (to give the property its more correct name) is due to the penetration of EM waves into the conductor. It is not “due to the magnetic fields”. Metals behave as a high loss dielectric with a very high refractive index. A better description is that the currents are induced by the EM wave that is refracted into the metal as a result of the ‘incident’ external field which carries the signal energy.
“The result is a loss of cable performance that can be measured as well as heard.“
It seems unlikely that this statement is true in general terms since the effects upon audio signal propagation are often very small. It might be better if they had said, “the effect may be measured, but will probably often have no audible significance”
“As a means of bypassing the skin effect and current bunching problems associated with cylindrical conductor designs, some cable manufacturers have developed rectangular conductors as an alternative.“
This is may be true, although it is not clear if this is a good topology. For what it is worth ‘suspended stripline’ and similar types of guide based upon rectangular conductors is used with RF/microwave systems for frequencies up to 10GHz and above.
“A solid rectangular conductor of this type is undesirable because the sharp corners produce high electric field values that over time can break down the dielectric, causing a failure of the cable”
I have not heard of occasions when this has lead to dielectric damage at the power levels that are relevant here. However it is correct that sharp corners will concentrate the E-field. The currents will also flow preferentially in the corners when the nominal skin depth is smaller than the dimensions of the conductor. Hence sharp corners may be inadvisible in some cases. However circular cross-section would avoid this potential problem.
“.·and this chafing can lead to a short that could conceivably damage your loudspeakers.”
I am not sure how a short produced by cable chafing would lead to loudspeaker damage. It would be more likely to provoke the protection circuits of an amplifier or lead to a problem with the amplifier. Again, I have not heard of this problem occurring in practice.
“Our engineers determined that a hollow oval cable constituted the best possible conductor design.”
“Best possible” here seems to be an opinion. I am not aware of any formal proof that could establish that no other geometry could not be “better”. Although of course, the term “best” may be being applied vaguely here, and just means “we liked it”.
“The primary advantage of an oval conductor design rather than cylindrical conductor geometry is that the oval shape allows more of the return current to be closer to the outgoing current, thus reducing the negative effects associated with excessive current bunching.”
In general terms, it is correct to argue that the higher radius of surface curvature of the faces of the conductors that are closest together will encourage the current to spread well. However it is not clear if “current bunching” is normally “excessive” in audio cables of more conventional design. If it is not, then the solution seems to be for a problem that does not matter in practice.
I am also not sure that some other geometry might not be more suitable. For example, an elliptic cross-section would avoid the curve-flat discontinuities of the oval. It would also probably be possible to analyse analytically by conformal mapping from the standard circular conductor twin feed arrangement. The analysis presented by Analysis Plus seems to be based upon numerical methods. These must be applied with great care as it is easy when applying such methods to make an error due to some hidden feature of the numerical code. The field and current patterns they use in their illustrations seem to be the results of models, not measurements. Hence although they are probably correct, they might not be.
“By using a hollow conductor, we help minimize the change in resistance with frequency and the cable becomes more efficient.”
The effect of hollowing is , of course, to increase the resistance at low frequency. Since the effects of internal impedance are likely to be small anyway it is not clear why making the low frequency performance nominally poorer is a good idea. In practice, though, it will not matter if the conductor has an adequate cross sectional area and diameter.
“Braided cable has yet another advantage over solid core conductors. Analysis Plus, Inc., uses a woven pattern in its Oval cables where every wire is statistically as close to the return current as every other wire. The current density is now more evenly distributed between the strands.”
In order for this to be assured it would be desirable for the individual strands to be individually insulated. If they are not, the current will simply tend to switch from strand to strand and seek to adopt the same overall distribution as it would have if the braiding were replaced by a solid conductor. However, if the braiding is made of individually insulated strands, and is woven/braided sensibly, then internal impedance variations would be suppressed without any need for an oval cross-section. Hence if what they say about their braiding is correct it implies that their hollow oval geometry is probably not required.
“The characteristic impedance of a cable is given by
where R is the series resistance, L is the series inductance, G is the shunt conductance, C is the shunt capacitance, and w is the angular frequency.
Note that this is not a simple number for a cable, but one which changes with frequency. It is also important to note that R, L, G, and C also change with frequency, making the impedance of a cable even more frequency dependent.”
The above statements should be treated with care in an audio context for a number of reasons.
Firstly, provided that the cable satisfies the Heavyside criterion (explained on the Scots Guide) then the cable impedance does not nominally have to change with frequency even if the cable has losses. Secondly, even for cables that do not satisfy the criterion, any effects at audible frequencies are likely to be very small. As with internal impedance they are are so small that it is questionable if they are audible in reasonably constructed cable. Thirdly, it is worth bearing in mind that domestic audio cables are very short in terms of wavelength, and are not used in a ‘matched’ situation. Hence the analysis implied by the above is not necessarily relevant.
Figure 3 on the Analysis Plus page shows cable effective resistance as a function of frequency. It is worth noting that the measurement is for a 100 foot length. They compare solid 12-gauge cable with their proprietary cables. (I assume this is a USA wire gauge which may differ from the UK one, but that does not matter here.)
At low frequency the indicated values for 12-gauge are around 0·2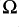
, rising to 0·5
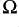at 20kHz. To make sense of these values we should consider a cable length that is more likely in a domestic situation. For the sake of a round value we can assume loudspeaker cables just 5 feet long (i.e. a 10 foot loop). This means a cable resistance of 20m
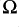at low frequency, rising to 50m
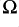at 20kHz.
When used with a 4Ohm loudspeaker load this implies a change in level between low frequencies and 20kHz of 0·065dB. This seems a small effect. Indeed, most loudspeakers will exhibit far greater imperfections in frequency response, and quite small movements of the speaker location (or listening position) in a room are likely to produce much greater effects. Also, the effects when using an 8 Ohm loudspeaker and/or shorter cables would be less. Thus the values Analaysis Plus give actually imply that 12 gauge may be fine and that their cable is solving a problem that is not actually of any audible concern.
“Z is a complex number, and it is common practice in the cable industry to simplify the situation by assuming a loss less transmission line and, in turn, assuming that R and G are zero. While this may be a valid approximation at high frequencies, it is not valid at low audio frequencies if you plan to construct an accurate model of a cable.”
Actually it is more likely to be a valid approximation at low audio frequencies than at high frequencies, so this statement seems the wrong way around. The meaning of “not valid” here also should be considered with some care. If the cables losses are so small as to be unlikely to have any audible effect it seems reasonable to regard the simplification as valid.
“For example, stating that a speaker cable has a constant, characteristic impedance of 10 ohms across the entire frequency range of 20 to 20,000 Hz is a drastic oversimplification that, in the end, is simply untrue.”
This statement is a curious one. The characteristic impedance of a loudspeaker cable isn’t a particularly useful value since the cable is not likely to be used in a matched environment, and the cable run is probably very small in wavelength terms. As a result, the behaviour of the cable will probably be dominated by its inductance and resistance. For these reasons it seems irrelevant to describe assumption of constant impedance as a “drastic oversimplification”. It might be better to say it was “largely irrelevant” to what is of interest here.
“Our Oval cables minimize frequency changes and boast a low impedance to reduce reflections at the high end of the audio frequency range.”
As indicated above, since the cable run is so short, the above statement seems to be not particularly relevant.
“Conventional cylindrical cable, due to its geometric limitations, typically has an impedance of about 100 ohms at the high end of the audio frequency band, thereby causing an impedance mismatch at high frequencies.”
The source (amplifier) and load (speaker) impedances are wildly different anyway. Hence this statement seems irrelevant. There would, for example, be no point in having cable which has a characteristic impedance of 8 Ohms since most loudspeakers (as their own data shows) won’t share this value, and the output impedance of most power amplifiers is well below 8 Ohms. The system is not intended to be used ‘matched’ hence their comment seems largely irrelevant. It would better to argue that low cable series inductance is useful in this situation.
Figure 4 compares the loop inductance of 12-gauge cable with their proprietary cable. Again the values shown are for 100 ft lengths and it makes sense to consider values for a more practical length. Taking a 5ft loudspeaker cable (10 foot loop) as before we have a value for the 12-gauge of around 2·2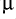 
H. It may be that I have missed something here, since the inductance will depend upon the wire spacing of the conductor pair. I have not noticed a value of conductor spacing specified for the 12-gauge example they use. This spacing will largely determine the inductance value. They may regard this as implicit in the description “12 gauge”, but if so I am not aware of the value.
An inductance of 2·2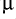
H corresponds to an impedance modulus of 0·27
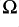at 20kHz. With a 4 Ohm load this would imply a change in power between low frequency and 20kHz of the order of 0·58dB. This is a modest change, but may be audible. However it is worth saying two things about this. Firstly, that only a tiny fraction of the inductance value they quote is probably due to internal impedance. Hence their concern with explaining the benefits of their own design in these terms seem irrelevant here. Secondly, if we look at some of the examples of twin feed loudspeaker cable on the Scots Guide we can see that it is possible to obtain lower inductance, if required, by a suitable choice of conventional twin feed. In general terms, we can minimise inductance by using a pair of wires which are close together compared to their diameters. Since they do not seem to give a value for the spacing of the ‘12 gauge’ they measure it isn’t possible to say if the value they measured could have been much lower if they had just moved the wires closer together.
From their figure 4 it would seem that they have obtained a reasonably low inductance per unit length. This is to be expected as they are using ‘flattened’ conductors in close proximity. The result will be a relatively low inductance, and of course, a correspondingly high capacitance. Similar results should, however, be obtainable using conventional twin feeder – perhaps using Litz wiring if suppression of internal impedance changes are required.
“Frequency Blurring
To minimize frequency blurring, it is important that the speaker cable parameters do not change with frequency. Ideally, the resistance and inductance would remain constant as the frequency of the signal changes. Figure 3 and 4 show that Analysis Plus, Inc., Oval cable minimizes the change of R and L with shifts in frequency, thus minimizing frequency blurring.”
The above is plausible in general terms, although the term “frequency blurring” is a vague one. However it seems likely that “frequency blurring” will be minimal anyway with a well chosen conventional twin feeder. Hence it is not clear from the above if the ‘solution’ they are offering is actually required in practice.
“While all real-world cables fall short of ideal behaviour in eliminating the problems of EMI, our Oval cables perform closer to the ideal than any other cable currently on the market. ”
This statement seems not to be accompanied by any evidence that it is correct, nor any explanation of why it might be true. It seems doubtful given that co-axial constructions and shielded pairs seem rather more likely to offer good interference protection. Their comment about “low inductance” being important in a following sentence makes assumptions about the type of interference which may be incorrect in practice. Twin feeders (even hollow oval ones) may pick up local fields and RF, and generally do so rather more effectively than co-ax.
Their Figures 5 and 6 are presented as measurements of the cable performance, compared with “the leading large-diameter audiophile cable”. So far as I can see, they omit to tell us any of the actual characteristics of this cable, so their comparison mainly implies that another cable with unspecified properties may not be very good. Alas, they also seem to omit any mention of the frequency of the test squarewave, or of the load (apart from calling it “the speaker”). Without this information, it isn’t possible to assess their comparison and hence it has no real value.
I may have missed some details from the Analysis Plus page, and made some errors in the above, since this was written in a hurry. However I think the overall impression is that, whilst much of what they say is fine, the results do not show that they have a ‘solution’ which is required in practical terms. Furthermore, if the main concern is internal impedance, rather simpler solutions would probably be as good or better as a technical solution.
None of the above should be taken as passing a comment on the ‘sound’ of their cables. I have not heard their cables, nor measured them. Their cables may be of excellent quality, and you might find they make you system sound fine. However if so, I suspect the reasons have little to do with the technical arguments they put forwards on the page I have considered here.
