The easiest way to assess the nonlinearity of an amplifier is to use a sinewave as a test signal and see if the amp adds components at harmonics of the chosen input frequency. If it does, then the amp is showing nonlinear distortion. Keith Howard has already examined the implications of nonlinearity and the interpretation of distortion spectra.[1] The good news is that most people aren’t interested in listening to isolated sinewave tones, and acoustic instruments tend to create a series of harmonics. As a result, the harmonics generated by some forms of nonlinearity might simply produce an effect which either passes un-noticed, or may even be pleasing. So does it really matter?
Much of the music we enjoy uses harmony and counterpoint, and we tend to listen to many notes being played simultaneously in shifting patterns. Musicians and instrument technicians will be aware that tuning and pitch are quite complex topics. Many of us will be familiar with terms like ‘Equal Temperament’. This does not mean that the musician has an amiable disposition. It refers to a well established system for tuning musical instruments. There are many such systems, but even the most familiar of them can cause some surprising results...
To illustrate this I chose two examples of amplifier nonlinearity, each assuming the same form of gain device (valve) nonlinearity. One using one device in a “single ended” arrangement (SE) , and the other using two in a “push pull” (PP) or balanced arrangement. Figure 1 (above) shows the chosen transfer curves on the left with the red line indicating the SE example and the blue line the PP example. The broken line is straight and can be used to see how each curve departs from being perfectly linear. On the right, Figure 1 also shows the shapes of the resulting output waveforms if the input is a sinewave.
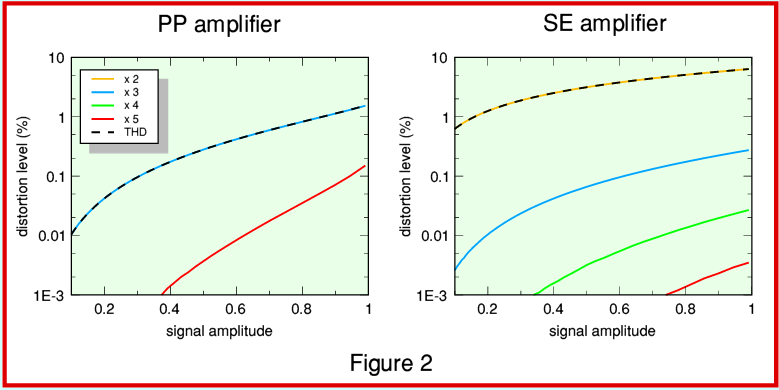
Figure 2 shows the levels of the harmonic components and the Total Harmonic Distortion (THD) levels for each of these examples. This represents the ‘classic’ test results showing how the THD varies with signal level. Comparing the harmonic distortion behaviours we can see that the SE arrangement exhibits much higher levels of THD (shown by the broken lines) than the PP arrangement. It can also be seen that the PP distortion is almost entirely due to the third order (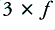
) distortion component, whereas the SE distortion is almost entirely second order (
).
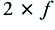Some enthusiasts for SE amplifiers argue that the nature of SE distortion is more benign than that of the PP arrangement. But what happens when we consider signal patterns more complicated than a simple sinewave...?
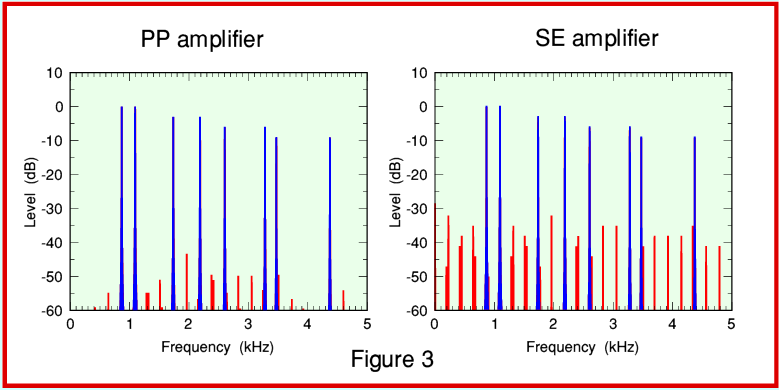
For the sake of investigation I decided to employ a test waveform that mimics two notes played as a chord. Each note consisting of a fundamental frequency plus four overtones (harmonics). The nominal pitches of these notes represent a major third consisting of an A and C# played together. Spectra of the results are shown in Figure 3. Components present in the input signal are shown in blue, with the ‘new’ components created by distortion shown in red.
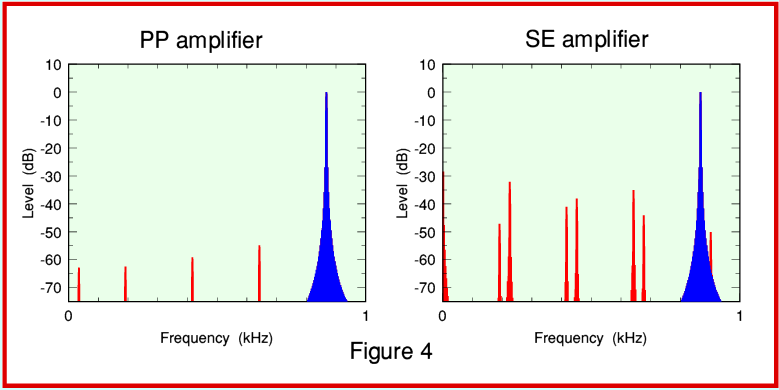
The precise levels of the distortion are – as we might expect – higher for the SE case than for the PP one. But the details differ significantly. We can understand these more easily if we ‘zoom in’ and only look at the frequency range up to 1 kHz as shown in Figure 4. To make the situation clearer, note that the vertical scale has also been extended so that smaller components become more easily visible. We can now see that the distortion spectra are quite different. The SE case exhibits a series of ‘paired’ components that were not present in the original signal, and these do not have a simple harmonic relationship with the fundamental frequencies of the input notes. There are two features of the SE distortion spectrum which may be particularly interesting.
One is the appearance of a ‘d.c.’ component which indicates how the asymmetric distortion tends to generate low frequency output. This indicates that as the amplitude of the musical waveforms vary, the SE nonlinearity tends to create an accompanying low frequency component that may behave like adding a ‘play along’ bass line! The other is the distortion component that appears very close to the fundamental tone of one of the input notes. Components which are close together like this can cause roughness or other changes to the sound.
What should be obvious from the above examples is that we can’t assume the distortion simply alters the relative levels of the components that were present in the original input. As soon as the input waveform becomes musically complex then we can expect the nonlinearity to create ‘new’ components that were totally absent from the input. In this case the test waveform was a major third with overtones, tuned according to ‘Equal Temperament’. In fact, there are various tuning systems which musicians may choose to employ. Equal Temperament is a common method that is adopted to avoid problems that can arise with pitch and harmony.
In a ’natural’ or ‘true’ tuning system the frequency ratio of the fundamentals of the notes in a major third would be 5:4. Unfortunately, if we attempt to enforce this throughout our tuning we end up with octave intervals which are not 2:1 ! To avoid this, Equal Temperament adopts a frequency ratio of 2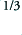
:1 for a major third – i.e. 1·25992:1 or 5·03968:4. The result of using such tuning systems, and the presence of harmonics in the musical tones, is that the intermodulation distortion products can be at frequencies that have no simple integer relationship with the individual notes!
I have, more than once, seen arguments to the effect that SE arrangements, or those with no overall feedback, “May have higher distortion, but this does not matter as they preserve the harmonic content, and hence the tambe (sound quality) of the music.” Alas, as the above results show, this argument simply doesn’t hold water unless we only listen to one note at a time and avoid anything but the simplest chords using perfect integer ratios! When lower order components of the THD dominate (as in the SE example) the result when playing a single tone or note will mainly be to slightly alter the relative levels of phases of the harmonics in the note. In such cases, these alterations may be ‘harmless’ in terms of perceiving the sound of the note, and similar to having a slight alteration in frequency response. However as the above examples show, this argument breaks down with more complex musical fare. The asymmetric SE arrangement now produces a complex set of anharmonic distortion products, and produces more of them, at a higher level, than the PP arrangement. The resulting alteration may sometimes be pleasing, but is it fidelity?...
Jim Lesurf
1200 Words
1st Dec 2006
[1] Weighting Game. Keith Howard Hi Fi News p64 December 2001
Phase Contrast. Keith Howard Hi Fi News p78 July 2003
Weighting up. Keith Howard Hi Fi News p78 March 2005
‘
