If you tend to read a variety of audio magazines then you sometimes encounter statements like
- “Analog systems like LP have infinite resolution and can reproduce infinitesimally tiny details of the audio.”
- “Digital systems like audio CD (CD-A) have a level of distortion that rises when the audio signal level falls below about -60dBFS.”
However – until now – you may not have noticed that you are unlikely to read such statements in Hi Fi News...
If true, these statements mean that LP has a greater ability to record and replay details than CD-A. This would be quite significant. So what do the above statements mean, and are they accurate?
If we look in typical relevant textbooks and at papers in academic journals on Information Theory or Communications Theory [1] we can find formal mathematical proofs that show that the first statement is either misleading or plain false. However, rather than getting bogged down in mathematics, we can see why this is the case by using a simple example.
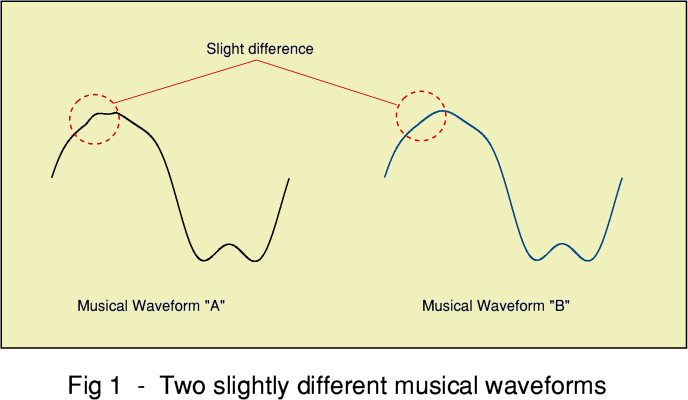
Consider two possible musical waveforms which are almost, but not quite, identical. These are represented by the waveforms “A” and “B” in Figure 1. Each waveform is used to make some LPs. We then play back two of these LPs when they arrive from the shop. However the LPs are only identified as “LP1” and “LP2”. The factory lost the paperwork, so we don’t have labels on the LP’s that tell us which of our LPs was produced using which initial musical waveform. Can we tell which is which? Indeed, can we even tell if we have a copy of both the different original waveforms?
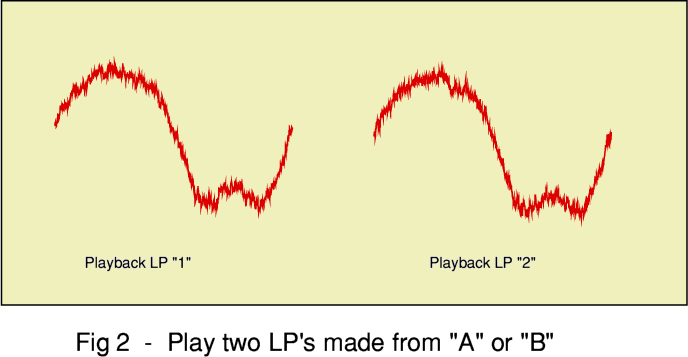
When we play the two LPs we get the results like those shown in Figure 2. In each case the replayed sounds are accompanied by random noise. The noise tends to obscure small details of the replayed waveforms. As a result, we may not be able to decide which LP was made from which original piece of music once the differences.
Some of the noise occurs due to random (thermal) motions of the atoms and electrons in the LP, and in the cartridge and amplifiers used to play the LPs. Some of the noise has been ‘built into’ the recordings due to similar random variations that occurred during the cutting, stamper manufacturing, etc, that were involved in making the LPs. From the physics of our universe, all of the real processes at each stage in an analog system like the LP will suffer from some level of these random effects.
The precise details of the signal and the noise will vary according to the circumstances. However the fundamental result is that as details of the intended signal become smaller they tend to become buried under the noise that is unavoidably present in all real systems. Hence we find that it is simply incorrect to assume that a real analog system like LP has “infinite resolution”. Tiny details will, once they are small enough, become undetectable.
In terms of Information Theory, the vital point here is that for two possible audio signals to be recognisably ‘different’ we have to be able to reliably distinguish one from the other. Alas, at some level the noise will obscure the details. In practice, no real-world system can have ‘infinite’ resolution. Noise sets a limit on the smallest details we can expect to record and replay.
Dynamic Range of CD-A
From the above we might expect that – for high fidelity – noise is always the ‘enemy’ and we would wish to reduce it to as low a level as possible, Surprisingly, however, this isn’t always the case. When making digital recordings the presence of some noise is often beneficial. It can provide a dithering effect that can wash away the problem known as quantisation distortion. I won’t look at that in detail here as it has already been discussed in the past in this magazine (e.g. [2] ) and I’ve also dealt with it on the web[3]. The references show how noise or dither can be used to remove quantisation distortion. The result is to allow digital systems like CD-A to behave like analog ones. Small signals do not become distorted, but as they become smaller they may eventually become buried in the noise. Provided noise or dither is used correctly, there is simply no need for CD-A signals below -60dBFS to show any actual distortion. They just sit above the noise level as they would in an analog system.
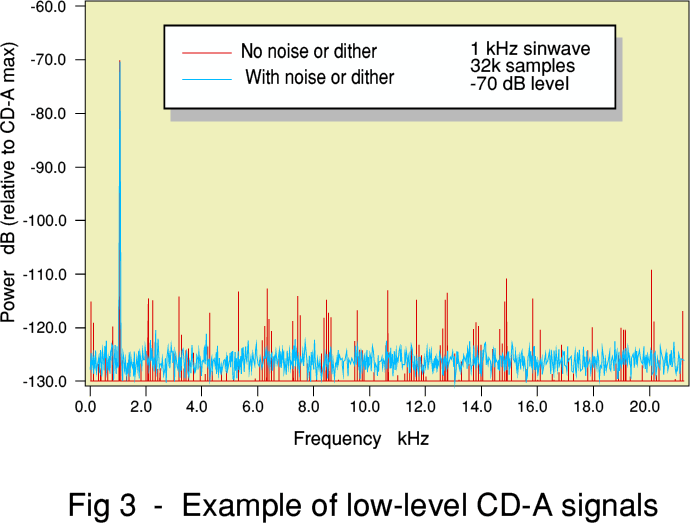
Of course, if we fail to ensure that the digital samples were correctly dithered, then then the results may be distorted. These results are illustrated in Figure 3. This shows a -70dBFS sinewave as a simple example, recorded as a series of CD-A format sample values. The red line shows what we get when no noise or dither were present. The blue line shows what we get when the input waveform was accompanied by some random noise, or we deliberately add this just before sampling. If we now remember that noise is a natural, and essentially unavoidable, accompaniment to any real-world sound recording, we can regard the red example as representing an ‘un-natural’ situation. Thus, although we can use something like a computer to generate a noise-free sinewave and set of samples (red line), this is an artificial test. The distortion-free result shown by the blue line is what we can expect (or arrange) to get when making audio recordings with due care.
In standard engineering terms the Dynamic Range (DR) of a signal carrying system is the ratio between the highest signal power the system will carry without significant distortion and the noise level. For CD-A, using noise or dither with a ‘white’ spectrum just powerful enough to remove quantisation distortion sets the noise level to be around -93dBFS. Ideally, CD-A recordings are arranged so that the maximum recorded signals never exceed the 0dBFS level, above which signals would become ‘clipped’. On this basis we can assign a DR of around 93dB to CD-A. For this reason you often see values around 90 - 96 dB quoted for the DR of CD-A.
Page 1 of 2
References for this page:
[1] A Mathematical Theory of Communication. C. E. Shannon & W. Weaver, University of Illinois Press, Champaign, Illinois
[2] Upsampling Again. Keith Howard, HFN pp 76-79 November 2002
[3] In a Dither, another AudioMisc article which you can go to by clicking here.