7. Effects of wire diameter and spacing
For all the examples considered so far we have used the same values of wire diameter and spacing. This has allowed us to compare various choices of conductor, etc, on a ‘like for like’ basis. In practice, however, one of the most common types of variation from cable to cable is in the choice of the diameters of the wires, and the spacing between them. We can now use a convenient standard material (Copper) and explore the effects of varying the spacing and diameter of the wires. As before we will assume a 3 metre length of twin-feeder, and an 8 Ohm resistive load as the standard for the purposes of comparisons.
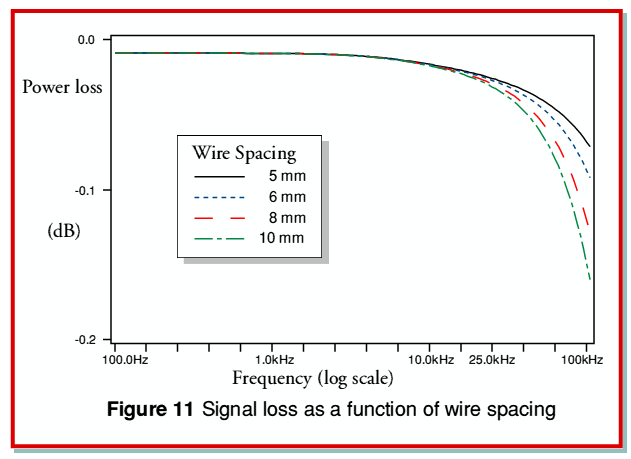
Figure 11 shows the effect of various choices of wire spacing, with a common wire diameter of 4mm (i.e. as previously, a wire radius of 2mm). Note that this has a different vertical scale to earlier power/frequency plots to accommodate the greater losses produced by the wider-spaced cables. Looking at the results we can see that the effect of moving the wires apart is to increase the relative loss at high frequencies. This is simply a consequence of the increase in wire spacing producing a corresponding rise in the cable’s inductance per unit length. The combination of the cable inductance and the load resistance act as a conventional 
low-pass filter. Since the wire diameter is the same for all the lines shown in figure 11 they all have the same value of wire internal impedance.
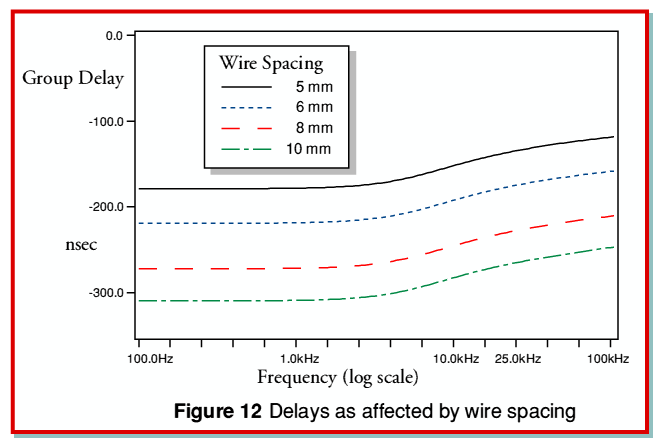
Figure 12 shows the time delay plots for the same set of spacings, etc, as used for Figure 11. As we would expect, as the spacing is increased and the cable inductance rises, the delay also rises. From the results shown in Figures 11 and 12 we can reasonably expect that we can generally hope to reduce the high frequency losses and overall group delay by choosing a small wire spacing and minimising the cable inductance.
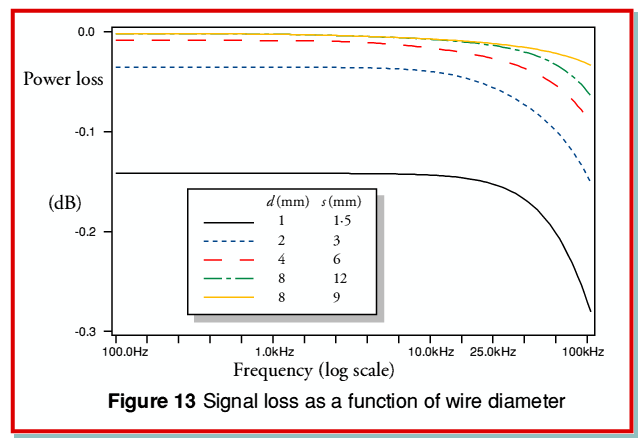
Having examined the effect of varying the wire spacing we can now look at the effect of the choice of wire diameters. Figure 13 shows the power loss as a function of frequency for our standard twin feeder, but using various wire diameters and spacings. Four of the plotted lines have the same wire diameter (d) to spacing (s) ratio. This is to ensure that they all actually have the same characteristic impedance and hence the same nominal inductance and capacitance per length. The variations between these four examples are therefore only due to changes in the internal resistance and inductance of the wires.
Comparing the four plots which share the same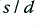 
value we can see that the lowest losses occur when the wire diameter (and hence spacing) is largest. This seems to clash with the desire to choose a low wire spacing. However the final plot (shown as a solid orange line) is for the largest wire diameter used for the previous four examples, but with a much smaller spacing. This reduces the inductance and hence reduces the level of high frequency power loss.
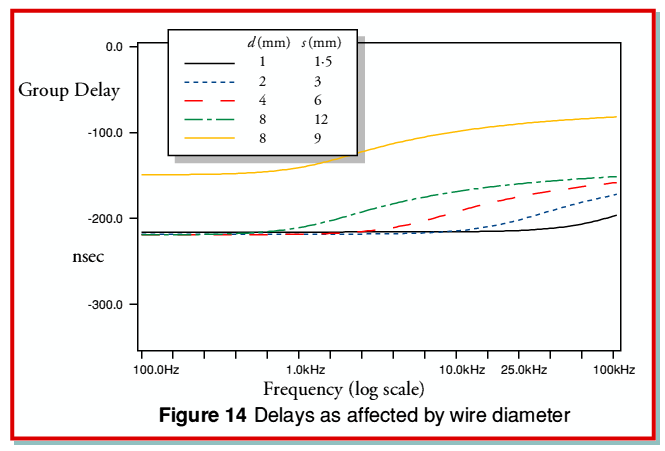
Figure 14 plots the group delays for the same cables as were used as examples for Figure 13. Looking at these it can be seen that for the examples which share the same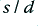 
value the smallest diameter tends to push the variation in delay as a function of frequency up into the ultrasonic range. Hence a small diameter might be desired if this result is wished. However, by using the thickest wires with a closer spacing we obtain the result shown with the orange line. This reduces the overall level of delay.
In practice it is questionable whether delays of the magnitudes shown would ever be audible. If so, the general advice would seem to be to choose reasonable large diameter wires with a close spacing in order to minimise the effects of resistance and inductance. Since the characteristic impedance of the cables tend to be low compared to those of a typical load the cable series resistance and inductance seem to have far more effect than cable capacitance. This being so, it is the cable resistance and inductance which we should regard as the primary threat to reliable signal transfer. If the change in group delay over the audio band is felt to be significant, a suitable remedy would be to adopt wires of Litz construction to reduce the change in internal inductance and resistance as a function as frequency. However it would still probably be good advice to ensure that each wire bundle was of reasonably large diameter, and the bundles were closely spaced.
