3. Effect of varying the cable impedance.
The example chosen for the previous section of this analysis had a nominal capacitance per unit length of around 55 pF/metre. This value arose as a consequence of the cable being chosen to have a characteristic impedance of around 75 Ohms, and the use of a reasonably low epsilon value (1·5) dielectric. In practice many types of coaxial cable used as domestic audio interconnects have capacitance per unit length value which are noticably higher than 50 pF/m. Hence it is useful to assess the effects of higher capacitance cables.
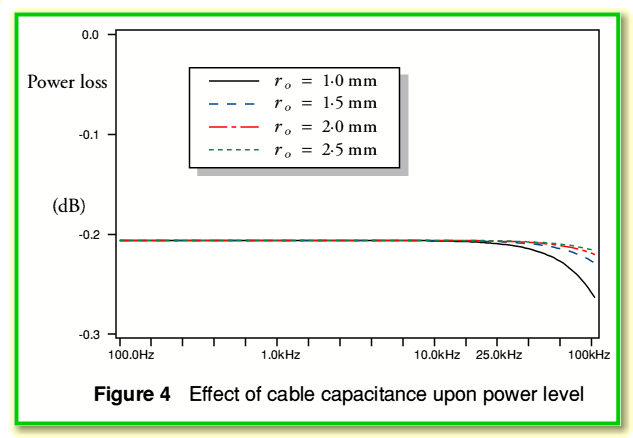
Figure 4 illustrates the typical effects upon the power loss as a function of frequency which may arise for four differing choices of cable capacitance per unit length. These examples use the same parameter values as before except for a change in the radius of the outer (shield) conductor. As before, the cable is assumed to be 2·5 metres long, and is driven by a 600 Ohm source, etc. The main changes here may be summarised in Table 1.
Table 1 - Signal Power Loss
| 
| 
| 
| 
| 
| 
| 
|
| 1·0
| 33.95
| 300·5
| 0·3466
| 120·2
| 0·1386
| - 0·206
| - 0·209
|
| 1·5
| 53·82
| 189·6
| 0·5493
| 75·8
| 0·2197
| - 0·206
| - 0·207
|
| 2·0
| 67·91
| 150·3
| 0·6931
| 60·1
| 0·2772
| - 0·206
| - 0·207
|
| 2·5
| 78·84
| 129·4
| 0·8047
| 51·7
| 0·3218
| - 0·206
| - 0·207
|
| mm
| Ohms
| pF
| 
| pF/m
| 
| dB
| dB
|
Looking at Figure 4 we can see signs that the effect of the cable does depend upon its capacitance. However the effect shown in these examples is mainly confined to high frequencies. Without any cable effects we would expect the combination of a 600 Ohm source and a 25 kOhm load to produce a potential divider power loss of 0·206 dB. Even at 25kHz the above examples show loss values which are within 0·003 dB of this value. Thus any other effects seems so small as to be likely to be unnoticable in practice.
To check the assumption that the differences in behaviour about 25kHz are due to capacitance we can also examine the time domain effects for the same set of examples as were used for the above.
Figure 5 shows the time delays the cables produce. In each case the delay can be seen to be quite uniform over the audio band. Table 2 summarises these results
Table 2 - Time delays
| 
| 
| 
| delay 1Khz
| delay 25kHz
|
| 1·0
| 300·5
| 180·3
| 176·1
| 176·1
| 176·1
|
| 1·5
| 189·6
| 113·7
| 111·1
| 111·1
| 111·1
|
| 2·0
| 150·3
| 90·2
| 88·1
| 88·1
| 88·1
|
| 2·5
| 129·4
| 77.6
| 75·8
| 75·9
| 75·9
|
| mm
| pF
| nanosec
| nanosec
| nanosec
| nanosec
|
Table 2 shows the calculated delays at 1 kHz and 25 kHz which take into account the cable internal impedances etc, compared with the nominal 
time constant value produced by the combination of the source resistance and the cable capacitance. In each case the agreement between the calculated 
value and the delays is reasonably good.
To obtain a better agreement we can take into account the fact that so far as the cable capacitance is concerned charge may enter or leave via both the source and the load. We should therefore regard the source and load impedances as being in parallel so far as the cable capacitance is concerned. When we take this into account the effective charge-path resistance seen by the cable will be 585·9 Ohms, not 600 Ohms. Column four of the table uses this resistance value to predict improved values for the system’s time constant. When we compare these new values with the predicted delays shown in columns five and six we can see that they are almost identical.
From the above we can draw some provisional general conclusions. The first is that for well behaved cables the loss and time delay values are likely to be highly uniform over the audio band. Secondly, that for the situations and cables considered the effects of internal impedance (including also d.c. cable resistance) seem to be so small as to make it doubtful that they are of any audible signficance. This does not exclude the possibility of some other effect influencing audio performance. Nor does it excude the possibility that inappropriately designed or built cables may degrade the signal transfer. However the cases analysed show far offer no support for claims that some cables offer improved performance for reasons related to “skin effects”.
The main implications are that the cable used should have reasonably low values for its capacitance and d.c. resistance per metre. From the above, a capacitance of around 100 pF/metre or less seems likely to be adequately low for interconnects that are no more than 2·5 metres long unless the source impedance is significantly higher than 600 Ohms. In practice, most good quality domestic audio sources are likely to have a source impedance below 600 Ohms, and the interconnects employed may often be only 1 metre in length. Thus even keeping to no more than 100 pF/m seems to be erring on the side of caution.
When the load impedance is much higher than the impedance of the source and the characteristic impedance of the cable the signal current is likely to be relatively small. Since this is true in most domestic systems it seems reasonable to expect that effects due to interconnect co-ax inductance, series resistance, and internal impedance should be very small, and it is questionable whether they are audible. Given its shielding properties co-axial cable seems a good choice for interconnect provided that we follow the general implications drawn above.
