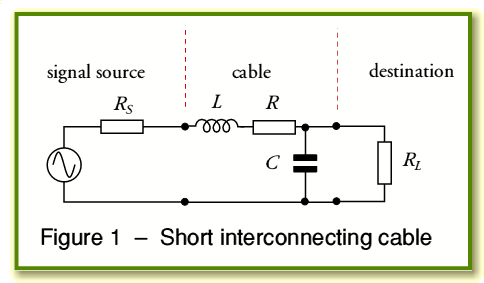
1. Simple model of coaxial interconnect.
These pages investigate the likely properties of coaxial cables when used as signal interconnects in an a domestic audio system. The basic properties of co-axial cable are considered in detail elesewhere. However we will concentrate on some specific examples.
The main properties of a co-axial cable are its inductance, capacitance, effective shunt conductance, and series resistance per unit length. Taken together these influence the signal transmission and loss properties when a length of cable is employed as part of a system. In the cases of interest here we can assume that the cable length will be far shorter than the wavelength of the audio signals. Hence we can treate the cable as a set of ‘lumped’ values. The main properties are
Nominal cable capacitance per unit length
Nominal cable inductance per unit length
D.C. resistance per unit length
Nominal shunt conductance per unit length
where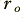 
represents the radius of the inner surface of the outer conductor, 
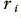represents the radius of the inner conductor, 
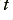represents the thickness of the outer conductor, and all the other symbols have their customary meanings. The impedance quantities are shown with primes to remind us that they are values per unit length. The double-primed epsilon indicates it is the loss part of a complex value.
At audio frequencies, and at the field levels appropriate for audio interconnects, we can reasonably expect that by using a suitable dielectic spacer (e.g. PTFE and dry air) we can obtain negligable shunt losses. The main potential source of problems which the above set of values omits is therefore the “skin effect”. We should therefore take this the internal impedance of the chosen conductors into account, but for now we may reasonably ignore delectric losses and disregard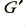 
.
Many of the details of internal impedance have been considered in other pages dealing with loudspeaker twin-feeder cables. Rather than repeat that here we can concentrate on the main differences between that situation and the one considered here. These may be summarised as follows
Firstly, we now have a different conductor geometry. As with twin feed, one conductor can be regarded as a wire of circular cross section. Hence its internal impedance will be given by an expression similar to that used for each of the individual pair of wires of a twin feed. However the outer conductor is a hollow cylinder and we must establish a relevant expression for its internal impedance contribution to the overall impedance properties of the cable.
Secondly, the source and load impedances may have values which can be chosen from a wide range. In the case of a twin feeder used for connecting a power amplifier to a loudspeaker we can usually expect the source and load impedances to be low relative to the cable’s characteristic impedance. This may often not be true for an interconnect. In general we can expect the load to have an impedance well above the characteristic value of the cable. In typical domestic systems the input impedance of amplifers (line level) may be between 10 kOhms and 100 kOhms. Similarly, the source impedance will often be below 1 kOhm (and may be below 10 Ohms) but may also be greater. In some cases the load may also have a noticable capacitance. We must therefore make reasonable allowances for this when assessing the overall effects of a given choice of co-axial interconnect.
Nominally speaking, co-axial cable is often used in an implicitly ‘unbalanced’ manner. i.e. it is assumed that the outer is held at ground potential and the potential of the inner wire is varied. Despite this is is usual to assume that the currents flowing in the inner and outer conductors are always equal in magnitude and opposite in sign. It is also usual to assume that the charge densities at any place on the inner and outer cancel to produce no net external effect.
In fact these assumptions are not always entirely justified. If both the signal source and its destination are earthed (grounded) by seperate wires then it becomes possible for a part of the “return” currents of signals to flow via these paths between the units. This may sometimes mean that the net EH fields outside the coaxial connectors are not zero. In addition, if the outer conductor is ‘thin’ (i.e. its radial thickness is not many times greater than the skin depth) some of the internal E-field may appear outside the outer conductor.
The above having been said, individual earth connections for units which can act as signal paths also tend to give rise to ‘ground loop’ hum effects. We would normally ensure that this does not arise in a well designed and properly used system. Hence we can hope that in most cases the internal current and charge values inside the co-axial cable balance well. We can also hope that in most cases the outer is of a reasonable thickness. This may mean that although there is a residual external E-field it will be evanescent and small. We may need to consider at some point the dielectric or conducting properties of materials nearby the cable. For now, however, we will assume the system is good enough that these effects can be ignored, although it may of value to consider them in detail later.
The value of the cable’s capacitance per unit length can be taken to be as given by expression 1 above. The resistance and inductance per unit length need to be modifed to take internal impedance into account. For the inner conductor we can use expressions virtually identical to those used for one conductor of a twin feeder and say that the internal resistance and inductance per unit length will be
where
and as before
is the skin depth, and
where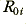 
is the d.c. resistance per unit length of the inner
The above results are based upon the analysis of Ramo and Whinnery. In a similar way we can use the results from the same text to say that the internal impedance of the outer will be given by the expressions
where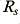 
is as given in expression 7 provided we use the same material for the inner and outer conductors. Note that these expressions assume that the thickness, 
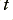, of the outer conductor is reasonmably small compared to 
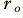. This assumption is generally reasonable. We can also usually expect the internal impedance contributions due to the outer to be smaller than those due to the inner. This is due to the outer having a larger radius and surface area. Hence a small inaccuracy in this should not have a significant effect upon the results we obtain provided we bear the assumption in mind.
We may now define the signal transfer system in terms of a lumped element circuit of the form shown in figure 1.
where we can now say that for a cable of length,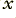 
, that
we can use the expressions to calculate the signal loss and delay as a function of signal frequency for any given choice of coaxial cable, source, and load.
