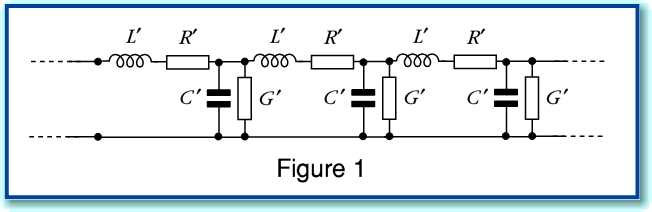
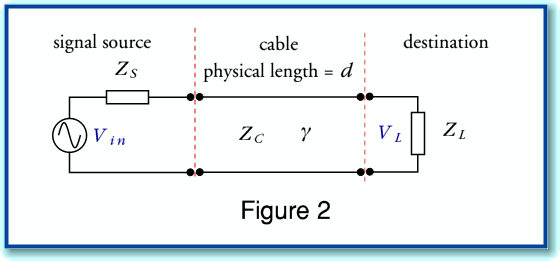
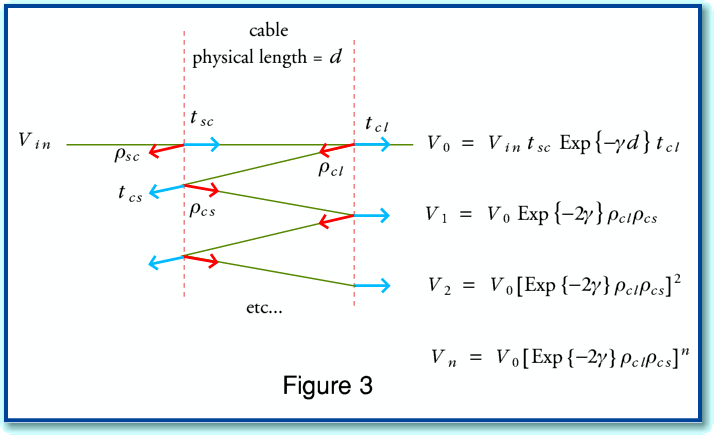
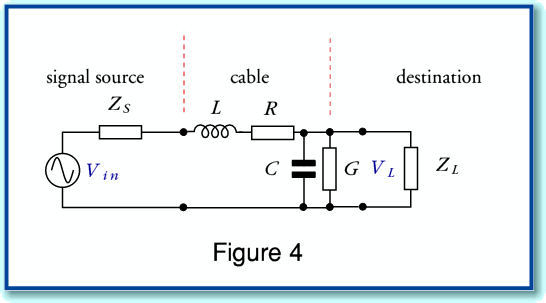
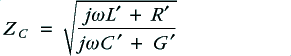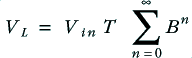Having defined the two models - analytic transmission line versus simple lumped approximation – we can now compare the results they predict is a situation of a kind appropriate for domestic audio. For the sake of example we can consider a 5 metre run of various loudspeaker cables with an 8 Ohm load. For simplicity, the source impedance is assumed to be essentially zero. i.e. the power amplifier has a high damping factor and negligible output impedance.
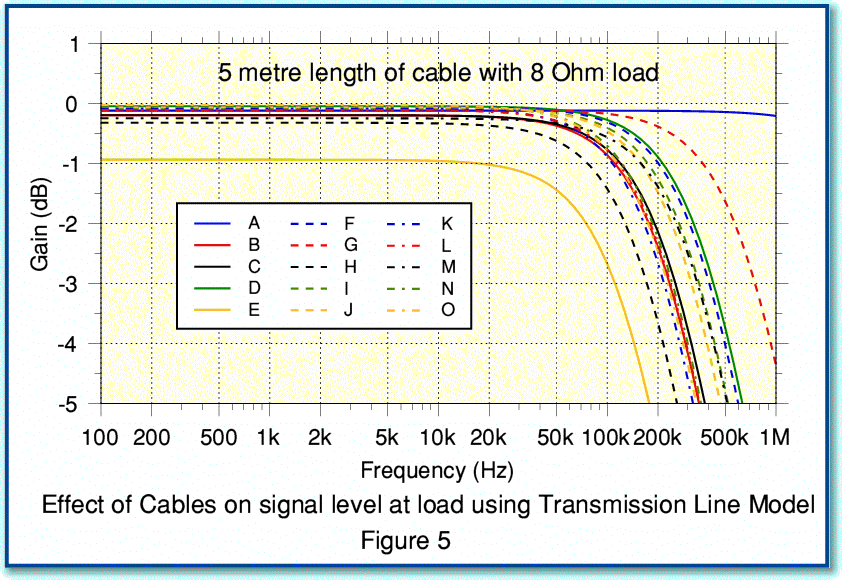
Figure 5 shows the change in signal level at the load predicted by using the analytical Transmission Line model. The results are for a random selection of 15 different loudspeaker cable designs whose RCGL values were measured and published in a survey in Hi Fi News some years ago. The measured values used in each case are listed in the table below.
Table of Cable Parameters
| Cable
|
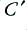 pF/m pF/m
|
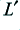 microH/m microH/m
|
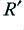 millOhms/m millOhms/m
|
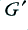 1/MOhm/m 1/MOhm/m
|
| A
|
1500.00
|
0.11
|
22.00
|
500.00
|
| B
|
34.60
|
1.06
|
36.20
|
250.00
|
| C
|
41.60
|
0.98
|
36.40
|
140.00
|
| D
|
170.00
|
0.60
|
8.40
|
55.00
|
| E
|
44.80
|
1.99
|
182.00
|
250.00
|
| F
|
88.00
|
0.63
|
10.60
|
67.50
|
| G
|
143.40
|
0.34
|
18.20
|
500.00
|
| H
|
20.00
|
1.42
|
60.00
|
150.00
|
| I
|
48.00
|
0.72
|
14.00
|
300.00
|
| J
|
48.00
|
0.80
|
11.40
|
85.00
|
| K
|
59.20
|
1.16
|
15.20
|
61.00
|
| L
|
58.00
|
1.06
|
20.00
|
55.00
|
| M
|
36.00
|
0.72
|
46.00
|
500.00
|
| N
|
28.00
|
1.04
|
7.60
|
250.00
|
| O
|
26.40
|
1.11
|
4.60
|
165.00
|
You can see that changing the cable can alter the frequency response in the region above 20 kHz, and alters the overall level at lower frequencies.
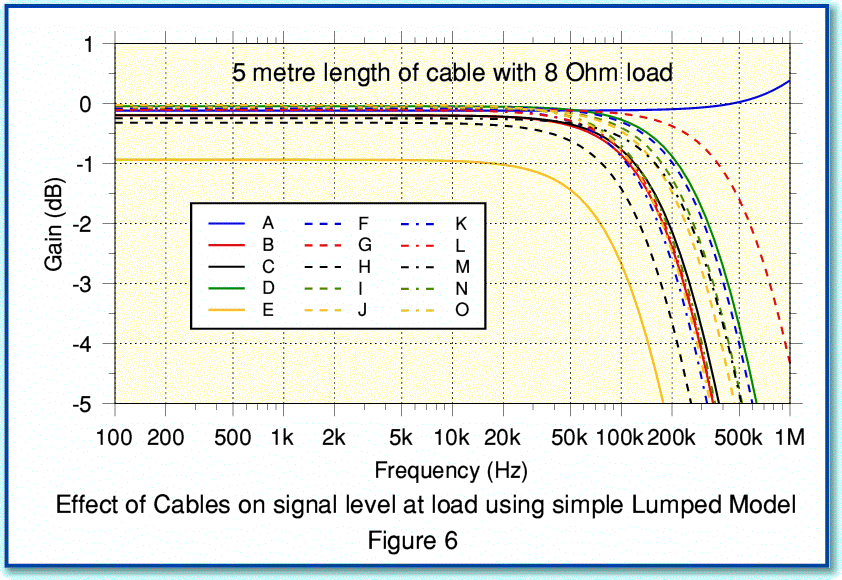
Figure 6 shows the changes in signal level for the same cable, but this time predicted using the simple Lumped Model. Comparing Figures 5 and 6 you can see some differences in predicted behaviour in the region above 20 kHz.
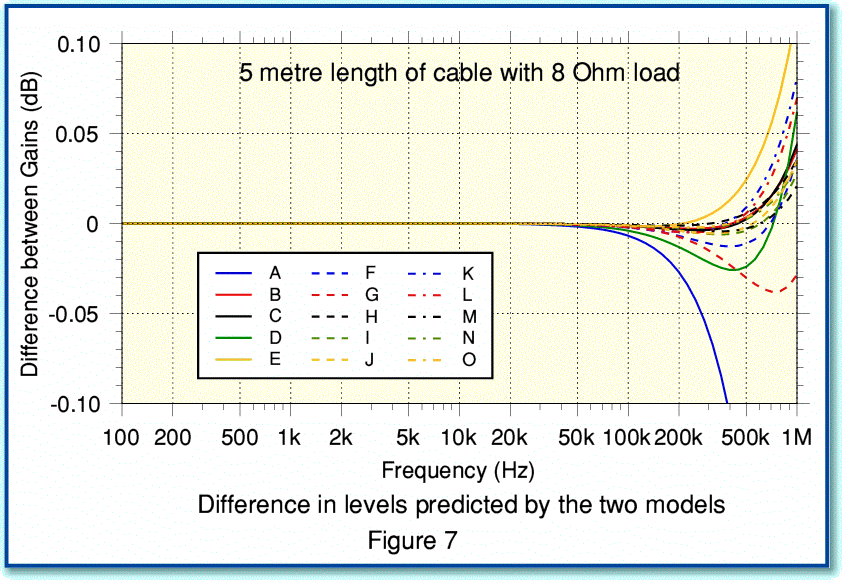
To make things clearer we can subtract one set of results from the other and display the differences. This will mean that 0dB will represent where the two methods give the same result, and any departure from 0dB indicates how much the two models disagree. The results are shown in Figure 7. Note the more sensitive vertical scale on this graph. From Figure 7 we can see that for our example conditions the two models produce much the same results for frequencies up to about 50 kHz. i.e. over a wider bandwidth that would be produced by most domestic audio sources. Even up to around 200 kHz the discrepancies between the two ways of predicting the effects of the cables give results similar to better than the 0.1 dB level.
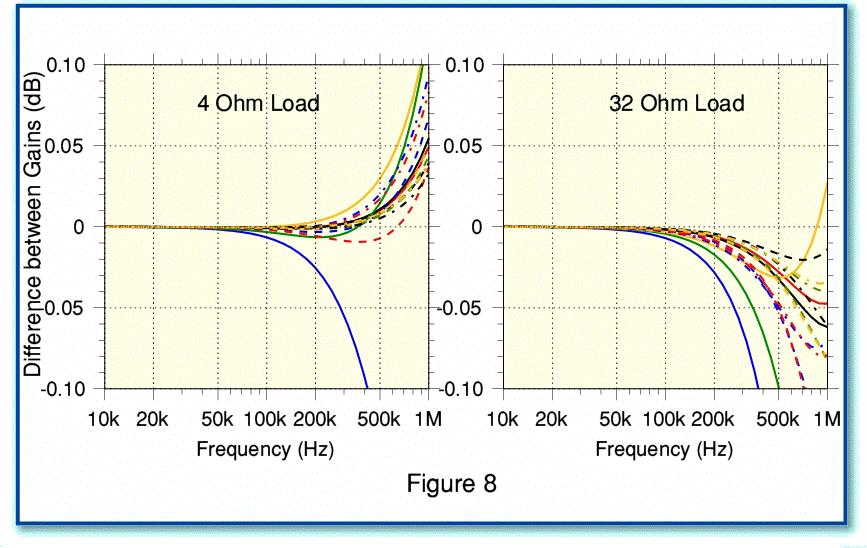
Figure 8 shows the difference in predicted levels for two alternative choices of test load using the same types and length of cable as previously. Although the details vary above 50 kHz you can see that these loads give the same basic behaviour as for 8 Ohms. i.e. that the two models give virtually identical predictions below about 50 kHz.
Of course, the above result might change if we used significantly longer cables, or loads whose impedance is nothing like 4 - 32 Ohms. But for cables somewhat shorter than 5 metres it seems likely that the simple lumped element approach will be fine for analysing the audio frequency behaviour of a cable. Hence in practice domestic loudspeaker cables a few metres long can be regarded as being short enough to for us not to need a transmission line analysis to model their effects upon signals at audible frequencies.
Jim Lesurf
28th Aug 2008