8.4 Special Purposes
On previous pages we have seen circuits which show how an op-Amp could be used as part of a feedback amplifier or filter. In fact, Op-Amps have many other uses and we can give a few examples here just to illustrate the range of possibilities.
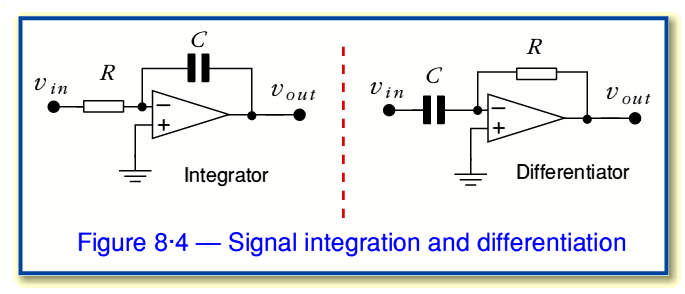
Figure 8·4 shows a pair of circuits which we can use to integrate or differentiate a signal value with respect to time. The Integrator acts to provide an output level proportional to the time-integral of the input level. It provides an output voltage at a time,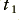 
given by
where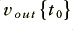 
represents the output voltage at some initial time, 
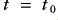, and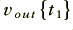 
represents the output voltage at a later moment, 
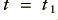. Note that the output is actually proportional to minus the integral of the input value 
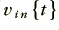, and that there is a constant of proportionality, 
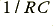. This arrangement is useful whenever we want to integrate or sum over a series of values of a signal over some period of time. In practice we often arrange to add a switch connected across the capacitor and close this, to set 
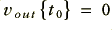and the instant we start the summing or integration. Signal integration is a very useful function in signal and data collection as we frequently wish to sum signal levels to improve a measurement by performing an average over many readings.
The Differentiator performs the opposite function. Here the output at some time,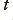 
, will be
This allows us to observe the rate of change of a signal level. (Note that the Differentiator here is a completely different function to the Differential amplifier we considered in earlier sections.) in both of the above circuits the scaling factor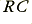 
is called the Time Constant as it has the dimensions of time and is often represented by the symbol, 
.
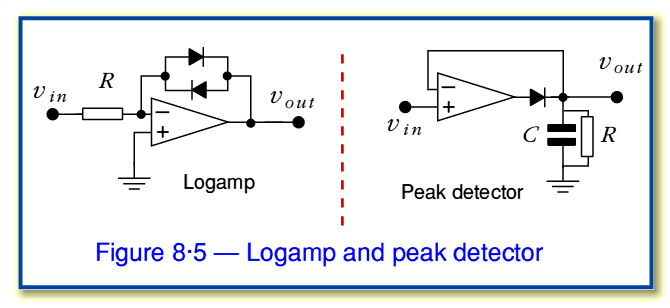
Figure 8·5 shows two examples of circuits which combine an Op-Amp with diodes to perform some useful non-linear function. The logamp exploits the fact that the effective resistance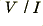 
of a diode varies with the applied voltage. For a ‘textbook’ diode we can say that the current and voltage will be linked via an expression of the form
where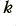 
is Boltzmann’s constant, 
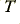is the absolute temperature of the diode, 
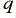is the charge on an electron, and 
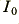is the saturation current value of the diodes chosen. In the logamp circuit shown in figure 8·5 a pair of diodes replace the usual feedback resistor.
Now the Op-Amp has a very high differential gain. This means that when it can it tries to adjust its output to keep its two input voltages very similar, and it also only draws a small input current. This means that the point where the resistor,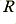 
, and the diodes meet will be held almost precisely at zero volts to ensure that the voltage at the inverting input almost exactly matches the zero potential applied to the non-inverting input. The low current requirement means that almost none of any current passing through the other components will flow in or out of the Op-Amp’s inputs. Hence we can say that the potential across the diodes will equal 
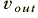and the potential across 
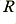will equal 
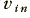. We can also expect the current in the pair of diodes to equal that through 
Since the diodes are connected in parallel, but facing opposing ways, the total current they pass when the output voltage is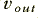 
will be
Whereas the current through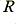 
will be 
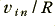. Putting these to be equal we therefore find that
Clearly under most circumstances this would be a truly awful choice for an amplifier as it will distort the signal’s time-varying voltage pattern quite severely. However its usefulness becomes apparent when we consider what happens when the voltages are large enough to ensure that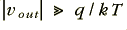 
. We can then approximate expression 8·6 to
which we can rearrange into
i.e. we find that when the signal levels are large enough the output voltage varies approximately as the natural log of the input voltage. Hence the circuit’s name Logamp. The circuit is very useful for Compressing the range of voltage levels. This means that amplitude measurements become easier to make, and signals easier to observe without becoming too small to notice or so large as to become overpowering. It can permit a system to work over a wider Dynamic Range. The sacrifice is that the actual signal pattern will be deformed in the process. By the way, note that the amplifier is still voltage inverting so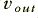 
always has the opposite sign to 
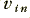. Also note that 8.8 is just an approximation and ‘blows up’ if you make the error of assuming it is correct when 
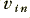approaches zero!
The second circuit shown in figure 8·5 acts as a positive peak detector. In this case the diode is being used as a ‘switch’ that can only pass current in one direction. The precise form of its nonlinearity doesn’t matter. The Op-Amp tries to behave like a voltage buffer and assert a voltage on the capacitor which equals its input. However it can only do this whilst the diode is prepared to conduct. Hence when the input is greater to or equal to the voltage on the capacitor the circuit behaves in this way.
However whenever the input voltage falls below the voltage on the capacitor the diode becomes reverse biassed. The Op-Amp cannot then force the capacitor to discharge.The charge stored can only leave via the resistor,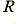 
. Hence the circuit tends to ‘remember’ most recent peak positive input voltage level, but slowly forgets unless the voltage rises to a new peak. If we wish we can remove the resistor and replace it with a switch. The output then always remains at whatever the peak positive value of the input has been since the last time the switch was closed. The circuit is therefore useful for holding peak values which only occur briefly. This function is useful in ‘peak hold’ meters and displays.
Summary
You should now understand the basic circuit arrangement used in most Op Amps and why it acts as a differential amplifier. The Class A output with small transistors also explains why most Op Amps can only output small current and power levels. You should now know how Op Amps can be used to perform various linear and nonlinear functions. These include the linear examples of tone controls, differentiators, integrators as well as the nonlinear ones of Logamps and peak detectors.
