The most obvious ‘limitation’ imposed by negative feedback is that the overall gain is reduced. As a result, when we want a lot of gain we may have to use a chain or Cascade of amplifiers. This will be more expensive, and require more space. At first glance it also looks as it will undo the benefit of low distortion since each amplifier in the chain will add its own distortions to the signal. Fortunately, this isn’t usually a real problem as we can see from the following example. Let’s assume that we have a basic amplifier design which – open loop – has a voltage gain of ×1000, and we want to amplify an actual input signal voltage by ×1000.
The simplest thing to do would be to use the amplifier, open loop, to provide all the gain. However in order to reduce the distortion we apply a feedback factor of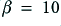 
, and then use a chain of similar stages, each with this feedback factor. The result still have an overall gain of 10×10×10 = 1000, but the feedback reduces the error level (and hence the distortion level) by a factor of 10/1000 = 0·01 in each stage.
The problem is that each stage adds its own distortion. We can therefore say that the total gain error of the chain of three amplifiers will be given by
(where we are assuming that the signal passes through the amplifiers in the order, ‘1, 2, 3’). Now when we obtain the same output level from the end of the chain as we would using a single stage with no feedback we can expect that
However the distortion levels produced by the other amplifiers are not equal to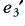 
. The reason for this is that the error (distortion) level varies with the size of the signal. In the middle amplifier. The signal level at the input/output of the middle amplifier (‘2’) in the chain will be 
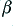times smaller than seen by ‘3’ at its input/output. Similarly, the input/output level seen by the first amplifier will be 
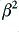times smaller than seen by ‘3’.
For the sake of simplicity we can assume that the error level varies in proportion with the signal voltage, hence we can say that
We can now approximate expression 4.14 to
i.e. for the values used in this example
i.e. we find that in practice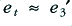 
and the overall distortion level tends to nearly all come from the distortions produced by the final stage.
In practice, the behaviour of a real system will be more complex but the explanation given above remains generally valid in most cases. As a result, a chain of feedback-controlled amplifiers tends to provide lower distortion than using a single stage without feedback despite the sacrifice in gain per stage. The only significant case where this result is not correct is when the error or distortion level does not fall with the signal size – i.e. if there is some kind of ‘kink’ or discontinuity in the amplifier transfer curve in the region around zero volts. In practice the situation where this arises is when we have used a pure class ‘B’ amplifier which will exhibit cross-over distortion. In these cases the feedback will reduce the distortion level for reasonably powerful signals, but small signals will experience high levels of gain error, and hence high distortion even when feedback is used. For this reason class ‘B’ should be avoided – especially when we are dealing with small signals – if we wish to avoid distortion.
From the simple explanation of feedback given in section 4·2 we might think that “the more, the better”. In practice, however, it is usually a good idea to only use a modest amount of feedback as excessive use can lead to some serious problems. The reason for this can be seen by looking again at expression 4·9 are remembering that in general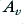 
, 
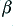, and hence 
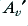will all be complex values. i.e. the gain and the feedback normally include some frequency-dependent phase/time effects as well as changes in signal amplitude. To see the consequences of this lets take another example.
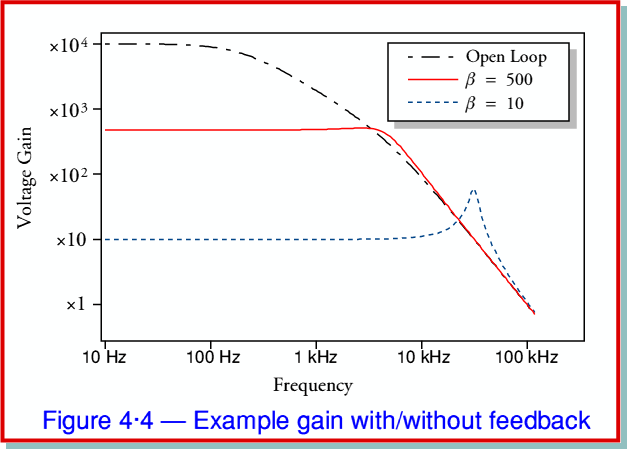
Consider a two-stage amplifier chain. Each stage has an open loop voltage gain of ×100 so the total low-frequency gain is ×104. However one of the amplifiers has internal stray capacitances that mean its gain tends to ‘roll off’ and behave as if it includes a first order low-pass filter with an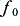 
of 200 Hz. The other amplifier has a similar limitation which gives it a turn-over frequency of 5kHz. We then measure the overall frequency response both with and without some feedback. The results will be as shown in figure 4·4.
The broken line with alternating long/short dashes shows the open loop gain of the system as a function of frequency. The solid (red if you see this in colour) line shows the frequency response with a feedback factor of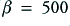 
, and the broken (blue) line shows the response with a feedback factor of 
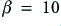. Looking at the graphs we can see that the 
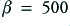feedback has the beneficial effect of ‘flattening’ the response and ensuring that the gain remains reasonably uniform over a wider range than is the case for the system without feedback. i.e. without feedback the response is only fairly flat up to a few hundred Hz, with with a feedback of 
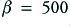applied the response is flat to nearly 10 kHz. Thus the bandwidth over which the amplifier can be used is increased by the application of feedback. In effect we have ‘flattened down’ the response, but it still almost fits inside the open loop response. Note, however that it doesn’t quite fit and that it slightly exceeds the open loop gain at high frequency.
It is customary to describe the amount of feedback applied to a system in terms of the ratio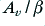 
. When this value is around unity the feedback does almost nothing. However as we reduce 
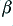in comparison with 
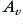the gain reduces, the distortion level tends to fall, and the flat bandwidth tends to increase. However if 
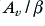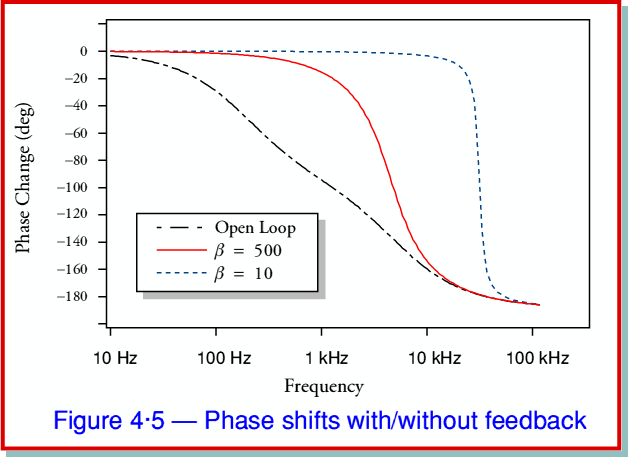
becomes too large things can go wrong as indicated by the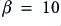 
line in figure 4·4. Here we can see that the frequency response has developed an odd ‘peak’ at around 30 kHz. The reason this happens can be understood by looking at figure 4·5 which displays the phase change versus frequency for each of the situations shown in figure 4·4.
Figure 4·5 shows two interesting points. Firstly, we can see that the feedback tends to suppress variations of the phase as a function of frequency just as it tends to reduce variations in the amplitude of the gain. However the second point is that this is only the case when the open loop phase change is less than about 90 degrees. In particular, looking at the graphs we can see that when the open loop phase change approaches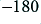 
degrees, the closed loop systems also move rapidly towards 
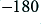degrees.
Now a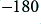 
degree change at a given frequency means that the complex gain has a negative sign. From before, we can say that the closed loop gain will be
however we may now find that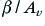 
is negative. Worst still, we may find that 
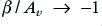. If this happens it means that 
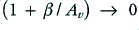, which in turn means that 
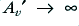. i.e. unless we take care we find that the feedback we intend to use to reduce the gain and make it more uniform may produce an unexpectedly high gain at a specific frequency (or set of frequencies) where we happen to have arranged for the above condition to arise! Since most of the effects which cause the open loop response to vary will affect both the amplitude and phase this problem is always potentially present. The more feedback we apply the wider the range of frequencies we bring into the intended ‘flat’ region, and the more chance there is for this problem to arise.
In fact we have encountered a consequence of what is called the Barkhausen Criterion. This says that we can make an oscillator by arranging for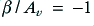 
. The peak at the end of the flat portion of the 
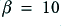response indicates that the system is near to becoming a 30 kHz oscillator. In practice, the load we may attach to the output of a real amplifier will tend to alter its gain behaviour, so if we allow the system to be ‘near’ oscillation we may find that it does oscillate under some circumstances when certain loads are attached. Avoiding this is particularly important in situations like hi-fi power amplifiers where the amplifier manufacturer can only be confident that a wide – even alarming! - range of loudspeakers with weird impedance behaviour will be used by various customers! An amplifier system which has a flat, unpeaked, response, with no risk of unwanted oscillations irrespective of the output load is said to be Unconditionally Stable. For obvious reasons this is highly desirable if it can be achieved.
To avoid these problems and ensure stability we have to adopt two approaches. One is to build an amplifier that works as well as possible without feedback, and then only apply a moderate amount. (Note that the terms “well as possible” and “moderate” here are matters of personal judgement not strict engineering.)
The second approach is to compensate the feedback or the amplifier to try and remove the problem. This can be done in various ways but two examples are as follows.
Firstly, we can adjust the amplifiers so that the open loop value of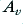 
has a magnitude of much less than unity at any frequency where the phase shift approaches 180 degrees. This make it very difficult for 
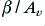to be able to approach 
.
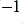Secondly we can apply lag/lead compensation. Up until now we have assumed the feedback circuit is just a pair of resistors. However we can add other components (capacitors or inductors) to the Feedback Network so that either the magnitude of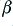 
or its phase change with frequency in a way that ensures a more uniform behaviour of 
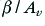as a function of frequency and keeps its value well clear of 
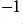at any frequency. The details of this process are outwith the scope of these pages, but you should see that these methods can help the situation, although the best policy is usually to avoid the problem by applying feedback with care.
Summary
You should now understand how Negative Feedback can be used to improve the performance of an amplifier system to give it a wider ‘flat response’ bandwidth and reduce the level of signal distortion. However it should also be clear that this feedback tends to reduce the available gain and has some associated problems. That the main limitations are of two kinds
- The risk of oscillations or instability
- Class B type distortions may not be reduced
We can use feedback with care to improve the performance of an amplifier, but it should be clear that although some feedback helps it is no substitute for designing or using an amplifier whose open loop behaviour is as good as possible.
