In part 2 we looked at some of the basic limitations of signal amplifiers, in particular power and signal size limitations. Now we will look at some of some of the other problems and see how a specific technique called Feedback can be used to deal with them. However, before doing so it is worth remembering that all ‘active’ systems use amplifiers. For example, the active filters we looked at in the last lecture require op-amps or similar amplifiers. What is less obvious is that amplifiers, in themselves, tend to act as filters...
There are two basic problems we want to examine in this section. The first is a consequence of the fact that all real components – resistors, capacitors, transistors, etc – suffer from what is know as ‘stray’ or ‘parasitic’ effects. For example, every real capacitor will have leads that have a non-zero resistance and inductance. Similarly, every transistor will have some capacitance between its leads, inductance in the leads, etc. As a result, every circuit we ever make will include lots of unintended, invisible ‘components’ which will affect the performance.
In addition, all real gain devices take a finite time to respond to a change in their input. For example, the ability of a bipolar transistor to pass current from its emitter to collector will depend upon the density of charges in its base region. When we change the base current it will take a finite time for the new current level to alter the charge density right across the base. It then takes another finite time before the emitter-collector current can react to this change. In bipolar transistors these effects are described in terms of an ‘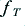 ’ value (transit frequency). This indicates the highest input frequency which will be able to change the output current. Higher frequencies tend to be ignored by the transistor as they change too swiftly for the transistor to be able to react.
’ value (transit frequency). This indicates the highest input frequency which will be able to change the output current. Higher frequencies tend to be ignored by the transistor as they change too swiftly for the transistor to be able to react.
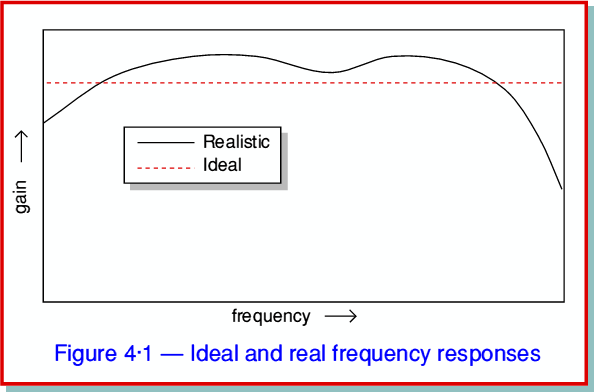
We don’t really need to worry here about all the detailed reasons for these effects. We can start from accepting that the result will always be an amplifier that will have a frequency response that isn’t just a uniform gain value at all frequencies. A real amplifier will be more likely to exhibit the complex kind of shape shown by the solid line in figure 4·1 than the ideal ‘flat’ response. In particular there will always be a tendency for the gain to fall at high frequencies. The phase/time delays may also vary with frequency. In addition, the complexity of the circuit (with all the stray effects) may mean that its frequency/time behaviour is far from uniform even at frequencies it can amplify reasonably well. The result of these effects is twofold. Firstly, the band of frequencies the amplifier can amplify may not be wide enough for our purposes. Secondly, the non-uniform gain/phase/time behaviour may alter the signal waveforms in a way we do not want. The signals can be distorted by non-uniform time/amplitude behaviour, although this term isn’t usually used for this effect.
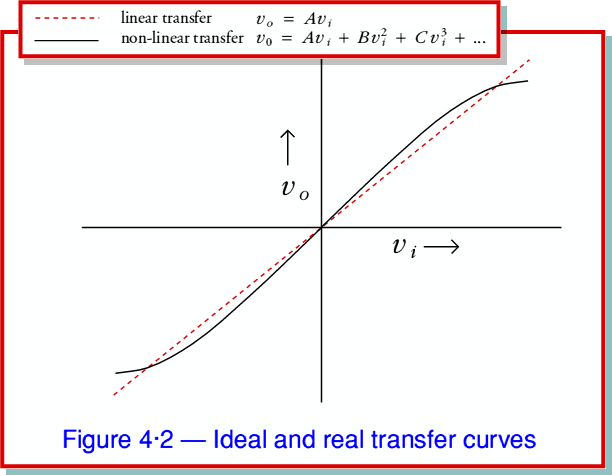
The term Distortion is usually used to mean that the amplifier has a gain which depends upon the signal amplitude (or sometimes also the frequency). The effect is described as an effect which arises due to non-linearity. Figure 4·2 illustrates the kind of non-linearity we are concerned with here. We can distinguish an ideal amplifier from a realistic one in terms of the Transfer Curve – the plot of 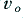 versus
versus 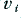 – and the expressions that relate the input to the output.
– and the expressions that relate the input to the output.
For an ideal, linear amplifier, the transfer curve will actually be a straight line, and we find that
i.e. the output level is simply proportional to the input and we can say that the amplifier’s voltage gain will be 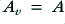 , a set value.
, a set value.
For a real amplifier, the transfer curve will not be a perfectly straight line. Now we have to represent the relationship between input and output using a more complicated equation. The most convenient form for our purpose is a polynomial, so we would now write something like
where the individual coefficients are constants for a specific amplifier. The result of non-zero values for 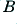 ,
, 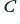 , etc means that the effective gain now becomes
, etc means that the effective gain now becomes
where since we can define 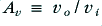 we can say that
we can say that
For a well-designed amplifier we can hope that the 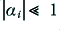 for all
for all 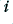 . This will mean the the amount of non-linearity, and hence the amount by which a signal is distorted during amplification, will be small.
. This will mean the the amount of non-linearity, and hence the amount by which a signal is distorted during amplification, will be small.