0 Introduction
There is a general, informal consensus that the choice of audio cable can often have an audible effect upon the perceived sound of a domestic Hi-Fi system. For this reason Hi-Fi enthusiasts frequently experiment with various types of cables and are willing to spend significant amounts purchasing cables which are claimed to provide high level of subjective performance. In recent years a sub-industry has grown out of these cables. In engineering terms, it is perhaps not surprising that the properties of a cable may affect the audio signals. Unfortunately, despite perceived subjective differences between cables, there has been little success in identifying the engineering factors that may determine these variation. There is also an absence of any established scientific basis for many of the claims which have been put forward by those who manufacture, espouse, or use these cables.
A recent set of three articles [1-3] by Duncan and Harrison in a popular UK Hi-Fi magazine have published a set of measurements upon 15 cables of differing types. These articles present data and claim that the authors have discovered that cables can impose a phase shift upon signals whose value varies with the rms signal current level. The data published indicates that the amount by which the phase shift alters with rms current may vary from cable to cable.
Since a level dependent phase shift would represent a signal distortion mechanism, the claims and data presented in the articles could – if justified – represent an important factor in the choice of cable. As a novel non-linear effect, this might also explain some subjective perceived differences which seem to be uncorrelated with any conventional parameters. Given the potential significance of the data and claims presented in the articles, it is therefore important to subject them to scientific scrutiny in order to see if they stand up to critical analysis.
1. The Measurement System
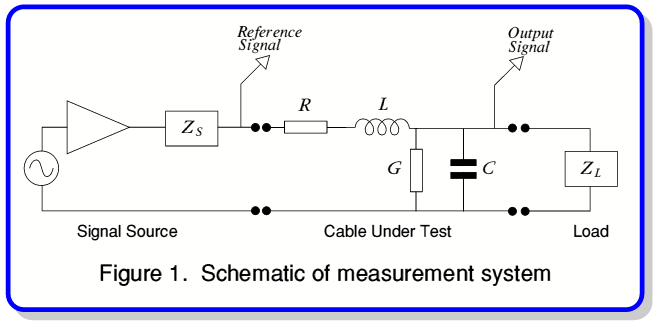
The measurement system employed to collect the phase measurements presented in the series of articles was quite complex, however for our purposes it can be simplified into the form shown in figure 1. Since the cables tested had physical lengths many orders of magnitude smaller than a quarter-wavelength at the frequencies used it seems reasonable to model the cable under test as a simple series resistance,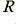 
, and inductance, 
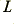, shunted by a leakage resistance, 
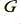, and capacitance, 
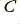. The source impedance can be represented by a value, 
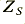, which is primarily a (small) inductance at the audio frequencies of relevance here. The load, 
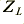, is nominally resistive. However this load was apparently connected to the cable under test via another length of cable. Hence the electrical properties of this additional cable may need to be taken into account when assessing the effect of the load upon the phase behaviour of the cable under test.
Sinewave signals were applied via the cable to the nominally resistive load. The frequencies chosen were restricted to the 1,000 - 1,500 Hz range. Two sets of phase measurements were undertaken on each cable. One being ‘low level’ (65mA RMS), and the other ‘high level’ (4·5A RMS). In each case the data was recorded in the form of a plot of phase delay versus frequency. Each data plot also included a nominal reference plot of the phase observed at the source end of the cable in an attempt to calibrate out any phase shifts elsewhere in the measurement system.
The recorded data clearly indicates a tendency for the phase shift at high current to be significantly greater than at low current. This implies that complex audio signals traversing the cables will be subtly distorted by current-to-phase modulation effects.
Upon first reading the articles, I was prompted to wonder what other effects might have given rise to the observed phase changes. Precision measurements of the kind presented are notoriously difficult and it is prudent to view any unexpected effects as being potentially due to simple system imperfections or methodology errors. Only when these have been eliminated can we safely conclude that a radical new effect has been discovered.
A consideration of the measurement system made me think of two main potential problems. The first was that the signal source might have an output impedance, or a transfer delay, which was level dependent. Given that an amplifier which is providing an output of 4·5A RMS is likely to be working harder than when it is providing 65mA, it seemed quite plausible that the driving amplifier might be the source of the observed level dependent phase change. To a first approximation, however, such problems might be expected to be taken into account by comparing the input (reference signal) and output phases and using their difference as the measured result.
The second obvious possibility became clear when the articles reported that the cable output load resistance was changed between the high and low current measurements. For the high current measurements a 4·1 Ohm load was employed. For the low current measurements a 16·05 Ohm load was employed. Changing the load in this way is potentially a weakness in the measurement methodology since it admits the possibility that the phase variations are due to the change in load, rather than the change in current.
So far as I was able to tell, this potential load-change effect was not addressed during the work reported in the articles. I therefore decided to analyse the published data to estimate what measured phase change would be expected as a result of altering the output load.
2. The Data
Here I will summarise the main, conventional, characteristics of the cables tested in the articles. Since their identities of the cables are not important here I will just number them. The values in table 1 are as given by the authors of the magazine articles.
Table 1 - Cable Lumped Parameter Values
| Cable
| R (milliohms)
| G (Gigohms)
| L (microhenries)
| C (nanofarads)
|
| 1
| 67.00
| 180.00
| 3.00
| 0.75
|
| 2
| 72.00
| 200.00
| 3.00
| 0.19
|
| 3
| 64.00
| 450.00
| 2.50
| 0.50
|
| 4
| 72.00
| 800.00
| 2.60
| 0.50
|
| 5
| 50.00
| 250.00
| 0.20
| 6.60
|
| 6
| 62.00
| 20.00
| 2.20
| 0.88
|
| 7
| 96.00
| 300.00
| 1.20
| 0.83
|
| 8
| 85.00
| 240.00
| 3.20
| 0.26
|
| 9
| 171.00
| 400.00
| 3.70
| 0.16
|
| 10
| 626.00
| 500.00
| 10.20
| 0.05
|
| 11
| 25.00
| 17.00
| 1.60
| 0.98
|
| 12
| 23.00
| 0.17
| 5.10
| 1.13
|
| 13
| 41.00
| 170.00
| 3.30
| 0.41
|
| 14
| 222.00
| 0.02
| 2.60
| 1.44
|
| 15
| 87.00
| 15.00
| 5.00
| 0.17
|
The phase measurements were summarised in the articles. However I decided to get as close to the ‘raw data’ as I could. I therefore made simple visual observations of the graphs printed in the articles to collect data values for the observed phase shifts at three frequencies, 1·0 kHz, 1·25 kHz, and 1·5 kHz, for each cable at each applied current level. Although this introduces an extra set of random errors due to the difficulty of reading the printed plots, it enabled me to approach the raw data rather than rely upon tabulated or interpreted results.
Phase values as a function of frequency are not a particularly clear way to assess any unusual cable or propagation effects. This is because a uniform propagation delay time will manifest itself as a frequency dependent phase change. Hence a small, non dispersive, propagation delay may mask any more interesting effects. For this reason I decided to convert the phase measurements into the time domain and perform the analysis there.
From first principles, a phase delay,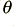 
, at a frequency, 
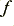, will correspond to a time delay of
where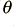 
is in degrees, 
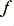in Hz, and 
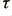will then be in seconds. (Degrees have been chosen here as the phase data plotted in the articles were in millidegrees.)
Table 2 summarises the values obtained from reading the plots, converted into time delays.
Table 2 - Cable Time Delays (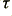
) in nanoseconds
| Cable
| 4.5 A
1 kHz
| 4.5 A
1.25 kHz
| 4.5 A
1.5kHz
| 65mA
1 kHz
| 65mA
1.25 kHz
| 65mA
1.5 kHz
|
| 1
| -611.11
| -600.00
| -583.33
| -138.89
| -133.33
| -92.59
|
| 2
| -777.78
| -777.78
| -777.78
| -194.44
| -200.00
| -166.67
|
| 3
| -527.78
| -533.33
| -537.04
| -111.11
| -111.11
| -111.11
|
| 4
| -638.89
| -644.44
| -648.15
| -138.89
| -155.56
| -111.11
|
| 5
| -55.56
| -44.44
| -18.52
| 111.11
| 44.44
| 74.07
|
| 6
| -472.22
| -466.67
| -462.96
| -111.11
| -111.11
| -74.07
|
| 7
| -194.44
| -200.00
| -203.70
| -27.78
| -44.44
| -18.52
|
| 8
| -722.22
| -688.89
| -129.63
| -111.11
| -133.33
| -111.11
|
| 9
| -750.00
| -733.33
| -740.74
| -166.67
| -177.78
| -148.15
|
| 10
| -1777.78
| -1777.78
| -1777.78
| -500.00
| -511.11
| -481.48
|
| 11
| -333.33
| -333.33
| -333.33
| -55.56
| -66.67
| -37.04
|
| 12
| -1000.00
| -1000.00
| -981.48
| -277.78
| -288.89
| -240.74
|
| 13
| -722.22
| -711.11
| -703.70
| -194.44
| -177.78
| -148.15
|
| 14
| -444.44
| -444.44
| -444.44
| -111.11
| -133.33
| -92.59
|
| 15
| -1055.56
| -1044.44
| -1055.56
| -277.78
| -288.89
| -259.26
|
The table clearly shows that there was an observed tendency for the delays at high current to be markedly greater than at low current. The articles assume this is evidence for an effect whereby the signal current level alters the cable signal delay.
The values shown in table 2 have already had the values of the observed input (reference) subtracted from them. This means that, so far as possible, the values shown exclude any external phase or time delays which arise elsewhere in the measurement system. This is convenient as it suppresses unwanted systematic errors. However it may not completely take into account the effect of the finite source impedance upon the cable/load behaviour. That said, the load impedance, and the characteristic impedance of the cables under test are far higher than the source impedance, so it seems reasonable to neglect this effect in the cases of interest here.
3. Simple Analysis
Here we can define the measured quantity,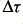 
, to be the observed difference in delay times when the current is changed. i.e. we can say that
For a perfect cable, driving a signal into a steady load, we would expect the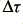 
value to be zero. i.e. we would not expect to observe a change in the time delay when altering the signal current level. Clearly, from table 2, this is not the case for the reported observations.
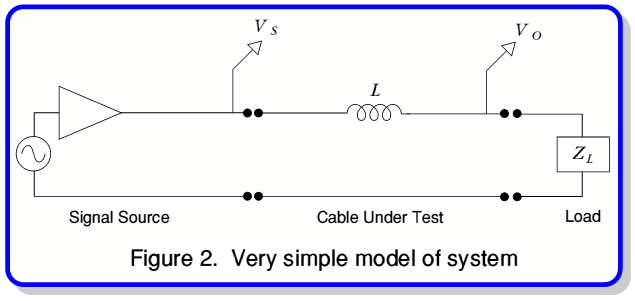
Let us now consider the interaction between the output load and the cable under test. We can begin by considering a deliberately over-simplified model which is presented for the sake of making a clear argument. In this simple case we neglect all cable parameters except its series inductance and assume the source has an impedance of zero. (i.e. is a perfect voltage source). As a result, the model will appear as shown in figure 2.
The phase delay produced by the cable/load interaction can therefore be obtained from the phase angle of the transfer ratio
Although nominally resistive, the output load was connected to the cable under test by another run of cable whose basic parameters were given in the article. Here, for the sake of clarity, we will initially ignore this and assume that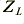 
is purely the specified load resistance. On this basis we would observe a phase change
There will therefore be a change in the observed output signal phase when we alter the load resistance value,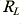 
, from one value, 
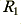, to another, 
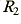. We can use this to define a computed time delay value which we would expect to arise,
It is obvious that this value depends upon the cable inductance,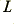 
. For low inductances we can expect the observed change in time delay with load to vary approximately linearly with cable inductance.
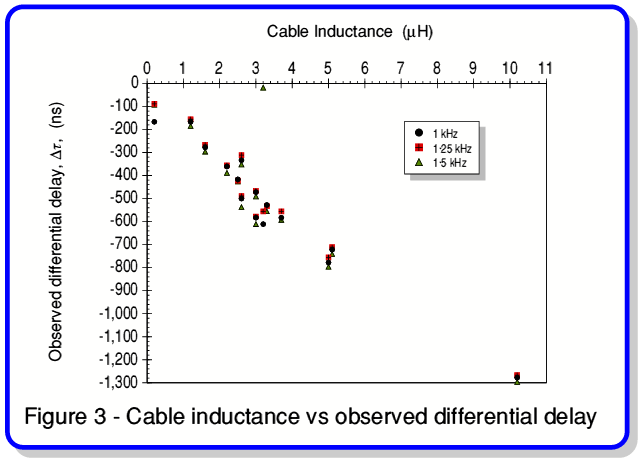
Figure 3 shows a graph of the measured cable inductance values plotted against the observed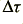 
values. The graph shows a clear trend whereby almost all of the points fall into a curve that implies a distinct relationship between the cable inductance and the observed change in phase with load (and hence with current). This result is quite encouraging given that a number of factors have been ignored for this simple analysis, and that the level of random errors in the data shown in table 2 is probably high. Although the trend displayed in figure 3 does not constitute any form of proof, it does support the hypothesis that the phase changes reported in the magazine articles may well be due to the interaction of the cable with the change in load, rather than the current.
In order to pursue this possibility a more detailed model of the system was constructed and its effects analysed. The time delays of this model could then be compared with the observed data reported in the articles.
4 A More Realistic Analysis
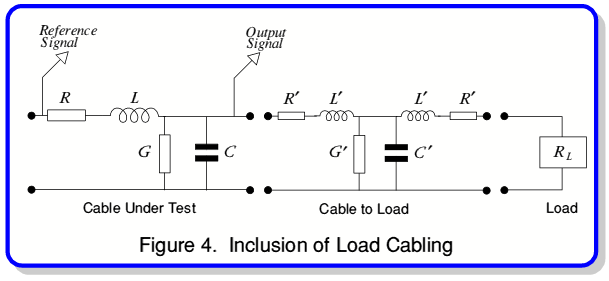
The more realistic model employed is shown in figure 4.
The measurements reported in the magazine articles specify that the resistive load was connected to the cable under test via another run of audio cable. This cable was apparently left unchanged during the measurements and consisted of a few metres of a specific cable. Using the values given in the articles we can model this as shown above with the values
The value of this cable’s leakage (shunt) resistance,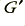 
, was not given in the articles. Here we can assume it was essentially infinite as it was likely to be many orders of magnitude greater than 
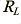. In this case it is appropriate to model the cable run as a T-symmetric lumped arrangement as we are interested in the interaction between the resistive load and the cable under test. However, an asymmetric model would be likely to give similar results given the very low frequencies employed compared those at which the cables would be a quarter-wave long.
A ‘C++’ program was written to compute the value of the total impedance of the load cable and resistive load, as seen by the cable under test. This value would correspond to
where the notation ‘//’ means ‘in parallel with’ and corresponds to
The cable under test will present a source impedance to the load of
The phase shift at the output end of the cable will then be equivalent to the phase angle of
which can then be translated into a time delay.
The program used the above approach to compute the predicted differential time delay,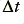 
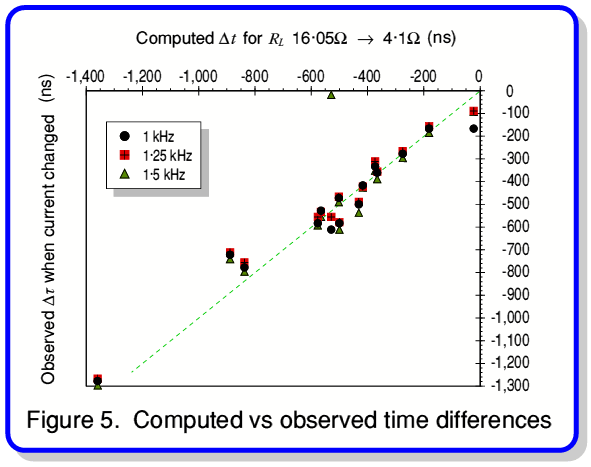
, that would be created at the output of the cable under test when the value of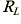 
was changed from 4·1 Ohms to 16·05 Ohms. Figure 5 shows a graph of these computed differential time delays against the differential time delay values, 
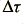, derived from the phase change with current reported in the magazine articles.
The broken line in figure 5 is of unity slope and passes through the origin. In the absence of any random or systematic errors every point would sit on this line if the model perfectly described the observed process. By looking at the plotted points we can see that the points do tend to sit fairly close to the line. Hence it seems at least plausible to conclude that the observed changes in phase with current are consistent with having been caused by the change in load which was made in order to alter the current level.
5 Conclusions
The main conclusion is that the results reported in the magazine articles do not require us to accept that cables can produce a signal phase or time delay which varies with the current level. Instead, the data reported seems quite consistent with what we would expect to occur as a result of the changes in load resistance made as a part of the measurement scheme. The observed phase changes therefore seem likely to be a consequence of an imperfection in the measurement methodology. No novel or unusual cable properties seem to be required. Standard transmission line and a.c. theory will suffice to understand the results obtained.
The fact that the reported observations can be modelled so easily does not, of course, constitute ‘proof’ that no new and unknown cable properties can possibly exist. Nor does it ‘prove’ that cables cannot affect the perceived quality of audio signals. However, it does indicate that the specific results reported in the magazine articles considered here do not require us to look for novel cable effects. So far as the cables themselves are concerned, the data only seems to imply that low series inductance and resistance will tend to minimise cable phase or time delays. This result seems unremarkable.
6 References
[1] The Great Cable Test – Part 1. Harrison, A., & Duncan, B.
Hi-Fi News & Record Review 30-41 44(7) July 1999
[2] The Great Cable Test – Part 2. Harrison, A. & Duncan, B.
Hi-Fi News & Record Review 32-41 44(8) August 1999
[3]The Great Cable Test – Part 3. Harrison, A. & Duncan, B.
Hi-Fi News & Record Review 40-53 44(9) September 1999
Click here to return to main Audio and Analogue page.
